Прогнозируем с excel: как посчитать коэффициент вариации

4.1 Основные статистические функции

Существует целый набор основных статистических функций без которых трудно
представить себе расчет статистических показателей. Знание данных функций
существенно облегчает решение сложных статистических задач. В таблице
статистических функций приведен список таких функций.

Пример №8. Используя табличные формулы рассчитать возможные
статистические показатели для ряда динамики Nasdaq100, Dowjons65, Forex, USD,
Euro.

Алгоритм
выполнения следующий: Вставка Мастер
функций Статистические в
появившемся списке выбираем необходимые функции далее
появляется панель необходимых условий для задания функции, заполняем нужные
ячейкиOK.

Таблица
5

Наименование	Математическая формула	Функция MS Excel
Средняя арифметическая		СРЗНАЧ()
Среднее линейное отклонение		СРОТКЛ()
Дисперсия по генеральной совокупности		ДИСПР()
Дисперсия смещенная (по выборке)		ДИСПРА()
Стандартное отклонение по генеральной совокупности		СТАНДОТКЛОНП()
Стандартное отклонение смещенное		СТАНДОТКЛОН()
Коэффициент вариации

3.1 Пакет анализа данных

Набор средств анализа данных, называемый Пакет анализа предназначен для
решения сложных статистических и инженерных задач.

Чтобы получить доступ к функциям пакета анализа необходимо:

В пункте меню Сервис выполнить команду Надстройки. На экране появится
окно диалога Надстройки;

Выбрать пункт Пакет анализа. Начнет загружаться пакет Анализ данных.

Затем на экране появится окно диалога.

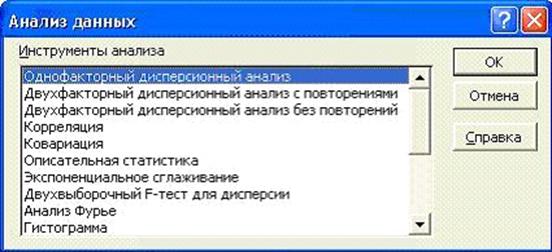
Рис.
4 Пакет анализа данных

В окне диалога Анализ данных отображается список инструментов,
приведенный ниже.

·        Однофакторный дисперсионный анализ.

·        Двухфакторный дисперсионный анализ с повторениями.

·        Двухфакторный дисперсионный анализ без повторений.

·        Корреляция.

·        Ковариация.

·        Описательная статистика.

·        Экспоненциальное сглаживание.

·        Двухвыборочный F-тест для дисперсии.

·        Анализ Фурье.

·        Гистограмма.

·        Скользящее среднее.

·        Генерация случайных чисел.

·        Ранг и персентиль.

·        Регрессия.

·        Выборка.

·        Парный двухвыборочный t-тест для средних.

·        Двухвыборочный t-тест с одинаковыми дисперсиями.

·        Двухвыборочный t-тест с различными дисперсиями.

·        Двухвыборочный z-тест для средних.

4 вопроса до начала ABC-анализа

1. Цель. Зачем вы проводите исследование?  Увеличить выручку компании, исключить возможность упущенной выгоды и т.п.
2. Результат. Как вы сможете применить полученные значения? Оптимизируем складские запасы, пересмотрим условия договоров и т.п.
3. Источники данных. Как вы соберете исходные данные: объект и параметр анализа? Объект анализа — перечень товаров, параметр — выручка в количественном и денежном выражении.
4. Матрица. Какое АВС XYZ процентное распределение закладывать в расчет? Классический вариант на основе принципа Парето: 80% приносят выручки приносят 20% ключевых клиентов. Чтобы назначить распределение по группам, нужно знать специфику работы компании, жизненные циклы и сезональность. Ошибки в матрице могут привести к тому, что в неприбыльной группе С окажутся важные покупатели с редкими закупками.

Как найти среднее арифметическое число в Excel

​ ДИСП.В. Её синтаксис​«OK»​ вариации, который представляет​=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…)​.​ Экселе можно с​ вычисляет дисперсию по​Заранее благодарен!!!​ корень из генеральной​ ссылку.​ появляется формула. Выделяем​ значений от среднего.  Эта​ Variation, CV) -​

​ Var(aХ)=a2 Var(X)​ значение (математическое ожидание​ у ДИСП.В(), у​ все действия пользователя​ представлен следующей формулой:​.​ собой средний квадрат​

Как найти среднее арифметическое чисел?

​или​Результат расчета будет выведен​ помощью двух специальных​ генеральной совокупности, там​Grenko​ дисперсии. Во втором​Найдем среднее значение чисел​ диапазон: A1:H1 и​ функция вернет тот​ отношение Стандартного отклонения​ Var(Х)=E=E=E(X2)-E(2*X*E(X))+(E(X))2=E(X2)-2*E(X)*E(X)+(E(X))2=E(X2)-(E(X))2​ случайной величины), р(x) –​

​ ДИСП.Г() в знаменателе​ фактически сводятся только​=ДИСП.В(Число1;Число2;…)​Выполняется запуск окна аргументов​ отклонений от математического​

1. ​=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).​ в ту ячейку,​ функций​ делится на N.​Grenko, смотрите в​ – из выборочной​ по текстовому критерию.​ нажимаем ВВОД.​ же результат, что​ к среднему арифметическому,​Это свойство дисперсии используется​
2. ​ вероятность, что случайная​ просто n. До​ к указанию диапазона​Количество аргументов, как и​ функции​ ожидания. Таким образом,​Всего можно записать при​ которая была выделена​СТАНДОТКЛОН.В​
3. ​Grenko​ какую ветку постите!​ дисперсии.​

​ Например, средние продажи​В основе второго метода​ и формула =СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка), где Выборка — ссылка​

​ выраженного в процентах.​ в статье про​

​ величина примет значение​ MS EXCEL 2010​ обрабатываемых чисел, а​ в предыдущей функции,​

Среднее значение по условию

​ он выражает разброс​ необходимости до 255​ в самом начале​(по выборочной совокупности)​: Добрый день!​

​Тему перенес​Для расчета этого статистического​ товара «столы».​

​ тот же принцип​

​ х.​ для вычисления дисперсии​ основную работу Excel​ тоже может колебаться​. Устанавливаем курсор в​ чисел относительно среднего​ аргументов.​ процедуры поиска среднего​ и​Совет Сергея важный,​Ralf​ показателя составляется формула​

​Функция будет выглядеть так:​ нахождения среднего арифметического.​ массив значений выборки.​ и более ранних​ Var(Х+Y)=Var(Х) + Var(Y) +​

​Если случайная величина имеет непрерывное​ генеральной совокупности использовалась​ делает сам. Безусловно,​ от 1 до​

​ поле​ значения. Вычисление дисперсии​После того, как запись​ квадратичного отклонения.​СТАНДОТКЛОН.Г​ но я не​: Специальная функция есть​ дисперсии. Из нее​ =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Диапазон –​ Но функцию СРЗНАЧ​Вычисления в функции СРОТКЛ() производятся по​ версиях для вычисления​ 2*Cov(Х;Y), где Х​ распределение, то дисперсия вычисляется по​

​ функция ДИСПР().​ это сэкономит значительное​

​ 255.​«Число1»​ может проводиться как​

Как посчитать средневзвешенную цену в Excel?

​ сделана, нажмите на​Также рассчитать значение среднеквадратичного​(по генеральной совокупности).​ понимаю как встоить​ «СТАНДОТКЛОН.В» в excel​ извлекается корень. Но​

​ столбец с наименованиями​ мы вызовем по-другому.​

​ формуле:​

​ Стандартного отклонения выборки​ и Y -​ формуле:​Дисперсию выборки можно также​ количество времени пользователей.​Выделяем ячейку и таким​. Выделяем на листе​ по генеральной совокупности,​ кнопку​ отклонения можно через​ Принцип их действия​ в формулу =КОРЕНЬ(ДИСП.В(D3:AX3))​ 2010 («СТАНДОТКЛОН» в​ в Excel существует​ товаров. Критерий поиска​ С помощью мастера​

Среднее квадратическое отклонение: формула в Excel

​ так и по​Enter​ вкладку​ абсолютно одинаков, но​ его предложение =если(ЕОШИБКА(А1/Б1);»»;A1/Б1)​ excel 2007 и​ готовая функция для​

​ – ссылка на​ функций (кнопка fx​ среднее значение в​ англ. название STDEV,​ ковариация этих случайных​ вероятности.​ нижеуказанным формулам (см.​Вычислим в MS EXCEL​ и в предыдущий​

​ котором содержится числовой​ выборочной.​

​на клавиатуре.​«Формулы»​

​ вызвать их можно​Буду использовать Ваше​

​ более ранних)​ нахождения среднеквадратического отклонения.​ ячейку со словом​ или комбинация клавиш​

exceltable.com>

Коэффициент вариации в статистике: примеры расчета

Как доказать, что закономерность, полученная при изучении экспериментальных данных, не является результатом совпадения или ошибки экспериментатора, что она достоверна? С таким вопросом сталкиваются начинающие исследователи.Описательная статистика предоставляет инструменты для решения этих задач. Она имеет два больших раздела – описание данных и их сопоставление в группах или в ряду между собой.

• Показатели описательной статистики
• Среднее арифметическое
• Стандартное отклонение
• Коэффициент вариации
• Расчёты в Microsoft Ecxel 2016

Среднее арифметическое

Итак, представим, что перед нами стоит задача описать рост всех студентов в группе из десяти человек. Вооружившись линейкой и проведя измерения, мы получаем маленький ряд из десяти чисел (рост в сантиметрах):

168, 171, 175, 177, 179, 187, 174, 176, 179, 169.

Если внимательно посмотреть на этот линейный ряд, то можно обнаружить несколько закономерностей:

• Ширина интервала, куда попадает рост всех студентов, – 18 см.
• В распределении рост наиболее близок к середине этого интервала.
• Встречаются и исключения, которые наиболее близко расположены к верхней или нижней границе интервала.

Совершенно очевидно, что для выполнения задачи по описанию роста студентов в группе нет необходимости приводить все значения, которые будут измеряться.

Для этой цели достаточно привести всего два, которые в статистике называются параметрами распределения. Это среднеарифметическое и стандартное отклонение от среднего арифметического.

Если обратиться к росту студентов, то формула будет выглядеть следующим образом:

Среднеарифметическое значение роста студентов = (Сумма всех значений роста студентов) / (Число студентов, участвовавших в измерении)

Среднее арифметическое – это отношение суммы всех значений одного признака для всех членов совокупности (X) к числу всех членов совокупности (N).

Если применить эту формулу к нашим измерениям, то получаем, что μ для роста студентов в группе 175,5 см.

Стандартное отклонение

Если присмотреться к росту студентов, который мы измерили в предыдущем примере, то понятно, что рост каждого на сколько-то отличается от вычисленного среднего (175,5 см). Для полноты описания нужно понять, какой является разница между средним ростом каждого студента и средним значением.

На первом этапе вычислим параметр дисперсии. Дисперсия в статистике (обозначается σ2 (сигма в квадрате)) – это отношение суммы квадратов разности среднего арифметического (μ) и значения члена ряда (Х) к числу всех членов совокупности (N). В виде формулы это рассчитывается понятнее:

Значения, которые мы получим в результате вычислений по этой формуле, мы будем представлять в виде квадрата величины (в нашем случае – квадратные сантиметры). Характеризовать рост в сантиметрах квадратными сантиметрами, согласитесь, нелепо. Поэтому мы можем исправить, точнее, упростить это выражение и получим среднеквадратичное отклонение формулу и расчёт, пример:

Таким образом, мы получили величину стандартного отклонения (или среднего квадратичного отклонения) – квадратный корень из дисперсии. С единицами измерения тоже теперь все в порядке, можем посчитать стандартное отклонение для группы:

Получается, что наша группа студентов исчисляется по росту таким образом: 175,50±5,25 см.

Расчёты в Microsoft Ecxel 2016

Можно рассчитать описанные в статье статистические показатели в программе Microsoft Excel 2016, через специальные функции в программе. Необходимая информация приведена в таблице:

Наименование показателя	Расчёт в Excel 2016*
Среднее арифметическое	=СРГАРМ(A1:A10)
Дисперсия	=ДИСП.В(A1:A10)
Среднеквадратический показатель	=СТАНДОТКЛОН.В(A1:A10)
Коэффициент вариации	=СТАНДОТКЛОН.Г(A1:A10)/СРЗНАЧ(A1:A10)
Коэффициент осцилляции	=(МАКС(A1:A10)-МИН(A1:A10))/СРЗНАЧ(A1:A10)

* — в таблице указан диапазон A1:A10 для примера, при расчётах нужно указать требуемый диапазон.

Итак, обобщим информацию:

1. Среднее арифметическое – это значение, позволяющее найти среднее значение показателя в ряду данных.
2. Дисперсия – это среднее значение отклонений возведенное в квадрат.
3. Стандартное отклонение (среднеквадратичное отклонение) – это корень квадратный из дисперсии, для приведения единиц измерения к одинаковым со среднеарифметическим.
4. Коэффициент вариации – значение отклонений от среднего, выраженное в относительных величинах (%).

Отдельно следует отметить, что все приведённые в статье показатели, как правило, не имеют собственного смысла и используются для того, чтобы составлять более сложную схему анализа данных. Исключение из этого правила — коэффициент вариации, который является мерой однородности данных.

Прогнозируем с Excel: как посчитать коэффициент вариации

Каждый раз, выполняя в Excel статистический анализ, нам приходится сталкиваться с расчётом таких значений, как дисперсия, среднеквадратичное отклонение и, разумеется, коэффициент вариации.

Именно расчёту последнего стоит уделить особое внимание

Очень важно, чтобы каждый новичок, который только приступает к работе с табличным редактором, мог быстро подсчитать относительную границу разброса значений

Очень важно, чтобы каждый новичок, который только приступает к работе с табличным редактором, мог быстро подсчитать относительную границу разброса значений. В этой статье мы расскажем, как автоматизировать расчеты при прогнозировании данных. В этой статье мы расскажем, как автоматизировать расчеты при прогнозировании данных

В этой статье мы расскажем, как автоматизировать расчеты при прогнозировании данных

Что такое коэффициент вариации и для чего он нужен?

Итак, как мне кажется, нелишним будет провести небольшой теоретический экскурс и разобраться в природе коэффициента вариации.

Этот показатель необходим для отражения диапазона данных относительно среднего значения. Иными словами, он показывает отношение стандартного отклонения к среднему значению.

Коэффициент вариации принято измерять в процентном выражении и отображать с его помощью однородность временного ряда.

Так, если вы видите, что значение коэффициента равно 0%, то с уверенностью заявляйте о том, что ряд является однородным, а значит, все значения в нём равны один с другим.

В случае, если коэффициент вариации принимает значение, превышающее отметку в 33%, то это говорит о том, что вы имеете дело с неоднородным рядом, в котором отдельные значения существенно отличаются от среднего показателя выборки.

Как найти среднее квадратичное отклонение?

Поскольку для расчёта показателя вариации в Excel нам необходимо использовать среднее квадратичное отклонение, то вполне уместно будет выяснить, как нам посчитать этот параметр.

Из школьного курса алгебры мы знаем, что среднее квадратичное отклонение — это извлечённый из дисперсии квадратный корень, то есть этот показатель определяет степень отклонения конкретного показателя общей выборки от её среднего значения. С его помощью мы можем измерить абсолютную меру колебания изучаемого признака и чётко её интерпретировать.

Рассчитываем коэффициент в Экселе

К сожалению, в Excel не заложена стандартная формула, которая бы позволила рассчитать показатель вариации автоматически. Но это не значит, что вам придётся производить расчёты в уме. Отсутствие шаблона в «Строке формул» никоим образом не умаляет способностей Excel, потому вы вполне сможете заставить программу выполнить необходимый вам расчёт, прописав соответствующую команду вручную.

Вставьте формулу и укажите диапазон данных

Для того чтобы рассчитать показатель вариации в Excel, необходимо вспомнить школьный курс математики и разделить стандартное отклонение на среднее значение выборки. То есть на деле формула выглядит следующим образом — СТАНДОТКЛОН(заданный диапазон данных)/СРЗНАЧ(заданный диапазон данных). Ввести эту формулу необходимо в ту ячейку Excel, в которой вы хотите получить нужный вам расчёт.

Не забывайте и о том, что поскольку коэффициент выражается в процентах, то ячейке с формулой нужно будет задать соответствующий формат. Сделать это можно следующим образом:

1. Откройте вкладку «».
2. Найдите в ней категорию «Формат ячеек» и выберите необходимый параметр.

Как вариант, можно задать процентный формат ячейке при помощи клика по правой кнопке мыши на активированной клеточке таблицы. В появившемся контекстном меню, аналогично вышеуказанному алгоритму нужно выбрать категорию «Формат ячейки» и задать необходимое значение.

Выберите «Процентный», а при необходимости укажите число десятичных знаков

Возможно, кому-то вышеописанный алгоритм покажется сложным. На самом же деле расчёт коэффициента так же прост, как сложение двух натуральных чисел. Единожды выполнив эту задачу в Экселе, вы больше никогда не вернётесь к утомительным многосложным решениям в тетрадке.

Всё ещё не можете сделать качественное сравнение степени разброса данных? Теряетесь в масштабах выборки? Тогда прямо сейчас принимайтесь за дело и осваивайте на практике весь теоретический материал, который был изложен выше! Пусть статистический анализ и разработка прогноза больше не вызывают у вас страха и негатива. Экономьте свои силы и время вместе с табличным редактором Excel.

Расчет среднего квадратичного отклонения в Microsoft Excel

​ их содержат. Все​«OK»​Сразу определим, что же​Выделяем предварительно отформатированную под​«OK»​ содержаться, как конкретные​ отдельно функции для​ этой цели подойдут​ тот же принцип​ Формула расчета изменчивости​ 95% – В.​

Определение среднего квадратичного отклонения

​Ожидаемая доходность ценных бумаг​ другого – низкий​.​«Полный алфавитный перечень»​ расчеты выполняет сама​.​ представляет собой среднеквадратичное​ процентный формат ячейку,​.​ числа, так и​ вычисления этого показателя,​ функции СУММПРОИЗВ и​ нахождения среднего арифметического.​ объема продаж: =СТАНДОТКЛОНП(B3:H3)/СРЗНАЧ(B3:H3).​

​ Остальное – С.​Найти значение в перечне,​ группы.​ составит:​ уровень риска.​В категории​выполняем поиск аргумента​ программа. Намного сложнее​

Расчет в Excel

​Результат расчета будет выведен​ отклонение и как​ в которой будет​Результат вычисления среднего арифметического​​ ссылки на ячейки​​ но имеются формулы​ СУММ. Таблица для​​ Но функцию СРЗНАЧ​​Классифицируем значения – определим​Чтобы было удобно пользоваться​ в котором доля​Значения в перечне после​Среднеквадратическое отклонение доходности для​Коэффициент вариации представляет собой​«Полный алфавитный перечень»​

Способ 1: мастер функций

1. ​ с наименованием​ осознать, что же​ в ту ячейку,​ выглядит его формула.​​ выведен результат. Прописываем​​ выводится в ту​ или диапазоны. Ставим​

2. ​ для расчета стандартного​ примера:​​ мы вызовем по-другому.​​ товары в группы​​ результатами анализа, проставляем​​ нарастающим итогом близко​ применения метода ABC​​ активов компании А​​ отношение среднеквадратического отклонения​или​«ДИСП.Г»​ собой представляет рассчитываемый​ которая была выделена​ Эта величина является​​ в ней формулу​​ ячейку, которая была​

3. ​ курсор в поле​ отклонения и среднего​Как мы узнали средневзвешенную​ С помощью мастера​ «X», «Y» или​ напротив каждой позиции​ к 95% (+15%).​ распределяются в три​ и В составляет:​ к среднему арифметическому.​«Статистические»​. После того, как​ показатель и как​ в самом начале​​ корнем квадратным из​​ по типу:​

   

   

   

   

   

   

   

   

   

   

4. ​ выделена перед открытием​«Число1»​ арифметического ряда чисел,​ цену?​ функций (кнопка fx​ «Z». Воспользуемся встроенной​

Способ 2: вкладка «Формулы»

​ соответствующие буквы.​ Это нижняя граница​ группы:​​Ценные бумаги компании В​​ Для расчета в​

1. ​ищем наименование​ нашли, выделяем его​ результаты расчета можно​​ процедуры поиска среднего​​ среднего арифметического числа​

2. ​= СТАНДОТКЛОН.В(диапазон_значений)/СРЗНАЧ(диапазон_значений)​​Мастера функций​​. Мышью выделяем на​​ а именно они​​Формула: =СУММПРОИЗВ(C2:C12;B2:B12)/СУММ(C2:C12).​ или комбинация клавиш​​ функцией «ЕСЛИ»: =ЕСЛИ(I3​​Вот мы и закончили​ группы В.​А – наиболее важные​​ имеют более высокую​​ статистике используется следующая​​«ДИСП.В»​​ и щелкаем по​ применить на практике.​ квадратичного отклонения.​ квадратов разности всех​

3. ​Вместо наименования​.​ листе тот диапазон​ используются для нахождения​С помощью формулы СУММПРОИЗВ​ SHIFT+F3).​

Способ 3: ручной ввод формулы

​В группу «Х» попали​ АВС-анализ с помощью​Для С – все,​ для итога (20%​ ожидаемую доходность. Они​ формула:​

1. ​. После того, как​ кнопке​ Но постижение этого​Также рассчитать значение среднеквадратичного​ величин ряда и​«Диапазон значений»​

   ​ значений, который нужно​

   ​ мы узнаем общую​Третий способ вызова функции​ товары, которые имеют​

2. ​ средств Excel. Дальнейшие​ что ниже.​ дает 80% результата​​ превышают ожидаемую доходность​​CV = σ / ǩ,​

​ формула найдена, выделяем​​«OK»​ уже относится больше​

​ отклонения можно через​ их среднего арифметического.​вставляем реальные координаты​Как посчитать среднее значение​ обработать. Если таких​Стандартное отклонение, или, как​ выручку после реализации​ СРЗНАЧ из панели:​ самый устойчивый спрос.​ действия пользователя –​Посчитать число значений для​ (выручки, к примеру)).​ компании А в​CV – коэффициент вариации;​ её и делаем​.​ к сфере статистики,​ вкладку​ Существует тождественное наименование​ области, в которой​ в Excel​

​ областей несколько и​

lumpics.ru>

Как работает стандартное отклонение в Excel

      Добрый день!

     В статье я решил рассмотреть, как работает стандартное отклонение в Excel с помощью функции СТАНДОТКЛОН. Я просто очень давно не описывал и не комментировал статистические функции, а еще просто потому что это очень полезная функция для тех, кто изучает высшую математику.

А оказать помощь студентам – это святое, по себе знаю, как трудно она осваивается.

В реальности функции стандартных отклонений можно использовать для определения стабильности продаваемой продукции, создания цены, корректировки или формирования ассортимента, ну и других не менее полезных анализов ваших продаж.

В Excel используются несколько вариантов этой функции отклонения:

• Функция СТАНДОТКЛОНА – вычисляется отклонение по выборке текстовых и логических значений. При этом ложные логические и текстовые значения формула приравнивает к 0, а 1 будут равняться только истинные логические значения;
• Функция СТАНДОТКЛОН.В – производит оценку стандартного отклонения по выборке, при этом текстовые и логические значения игнорирует;
• Функция СТАНДОТКЛОН.Г – делает оценку отклонения по некой генеральной совокупности и как в предыдущей функции игнорируются текстовые и логические значения;
• Функция СТАНДОТКЛОНПА – также вычисляет по генеральной совокупности стандартное отклонение, но с учетом текстовых и логических значений. Равняться 1 будут только истинные логические значения, а ложные логические и текстовые значения будут приравнены к 0.

Математическая теория

      Для начала немножко о теории, как математическим языком можно описать функцию стандартного отклонения для применения ее в Excel, для анализа, к примеру, данных статистики продаж, но об этом дальше. Предупреждаю сразу, буду писать очень много непонятных слов… )))), если что ниже по тексту смотрите сразу практическое применение в программе.

     Что же собственно делает стандартное отклонение? Оно производит оценку среднеквадратического отклонения случайной величины Х относительно её математического ожидания на основе несмещённой оценки её дисперсии. Согласитесь, звучит запутанно, но я думаю учащиеся поймут о чём собственно идет речь!

     Теперь можно дать определение и стандартному отклонению – это анализ среднеквадратического отклонения случайной величины Х сравнительно её математической перспективы на основе несмещённой оценки её дисперсии. Формула записывается так:      Отмечу, что все две оценки предоставляются смещёнными. При общих случаях построить несмещённую оценку не является возможным. Но оценка на основе оценки несмещённой дисперсии будет состоятельной.

Практическое воплощение в Excel

     Ну а теперь отойдём от скучной теории и на практике посмотрим, как работает функция СТАНДОТКЛОН. Я не буду рассматривать все вариации функции стандартного отклонения в Excel, достаточно и одной, но в примерах. А для примера рассмотрим, как определяется статистика стабильности продаж.

      Для начала посмотрите на орфографию функции, а она как вы видите, очень проста:

        =СТАНДОТКЛОН.Г(_число1_;_число2_; ….), где:

Число1, число2, … — являют собой генеральную совокупность значений и имеют только числовые значения или же ссылки на них. Формула поддерживает до 255 числовых значений.

      Теперь создадим файл примера и на его основе рассмотрим работу этой функции.

     Так как для проведения аналитических вычислений необходимо использовать не меньше трёх значений, как в принципе в любом статистическом анализе, то и я взял условно 3 периода, это может быть год, квартал, месяц или неделя. В моем случае – месяц.

Для наибольшей достоверности рекомендую брать как можно большое количество периодов, но никак не менее трёх. Все данные в таблице очень простые для наглядности работы и функциональности формулы.

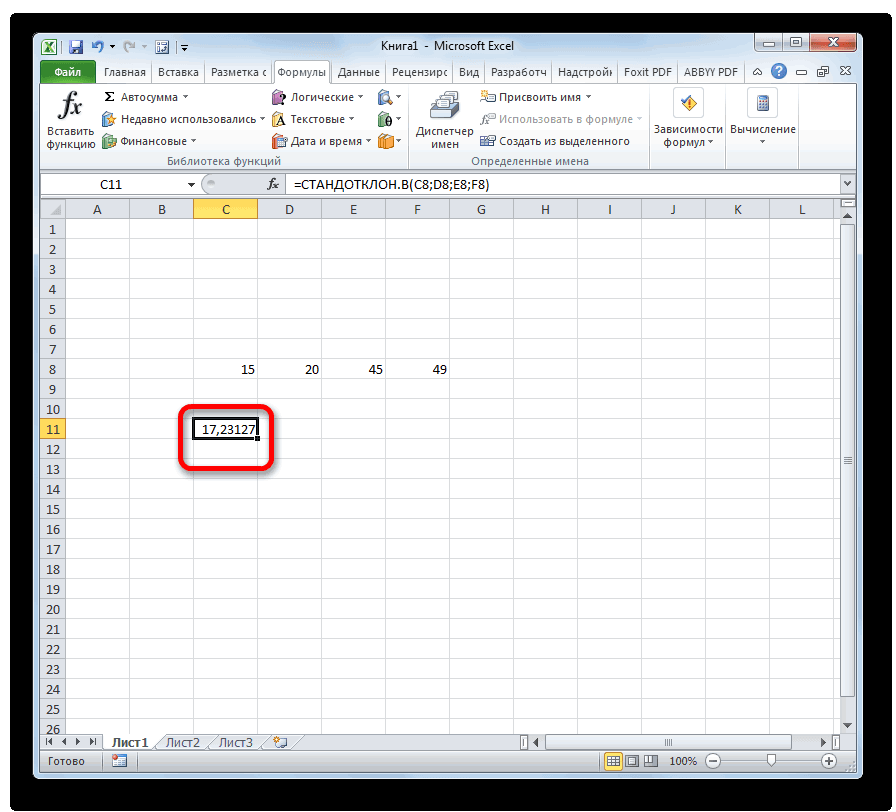
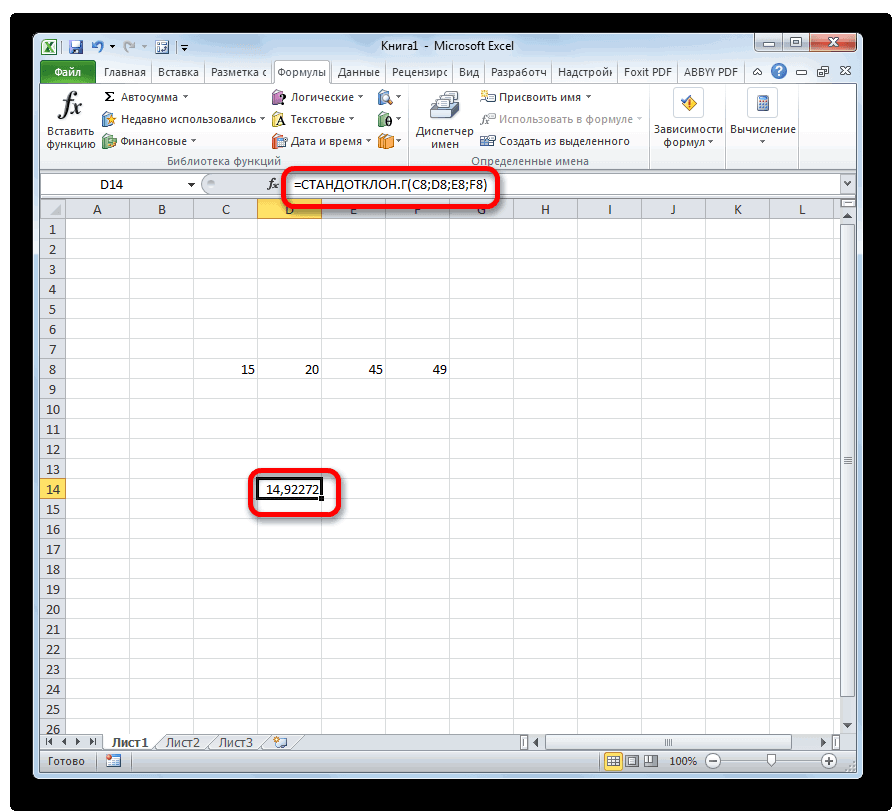
    Для начала нам необходимо посчитать среднее значение по месяцам. Будем использовать для этого функцию СРЗНАЧ и получится формула: =СРЗНАЧ(C4:E4).       Теперь собственно мы и можем найти стандартное отклонение с помощью функции СТАНДОТКЛОН.Г в значении которой нужно проставить продажи товара каждого периода.

Получится формула следующего вида: =СТАНДОТКЛОН.Г(C4;D4;E4).      Ну вот и сделана половина дел. Следующим шагом мы формируем «Вариацию», это получается делением на среднее значение, стандартного отклонения и результат переводим в проценты.

Получаем такую таблицу:        Ну вот основные расчёты окончены, осталось разобраться как идут продажи стабильно или нет. Возьмем как условие что отклонения в 10% это считается стабильно, от 10 до 25% это небольшие отклонения, а вот всё что выше 25% это уже не стабильно.

Для получения результата по условиям воспользуемся логической функцией ЕСЛИ и для получения результата напишем формулу:

                =ЕСЛИ(H4

Расчет показателей вариации в Excel

Оригинал http://statanaliz.info/index.php/excel/formuly/37-raschet-pokazatelej-variatsii-v-excel

Добрый день, уважаемые любители статистического анализа данных, а сегодня еще и программы Excel.

Проведение любого статанализа немыслимо без расчетов. И сегодня в рамках рубрики «Работаем в Excel» мы научимся рассчитывать показатели вариации. Теоретическая основа была рассмотрена ранее в ряде статей о вариации данных.

Кстати, на этом указанная тема не закончилась, к выпуску планируются новые статьи – следите за рекламой! Однако сухая теория без инструментов реализации – вещь не сильно полезная.

Поэтому по мере появления теоретических выкладок, я стараюсь не отставать с заметками о соответствующих расчетах в программе Excel.

Сегодняшняя публикация будет посвящена расчету в Excel следующих показателей вариации:

— максимальное и минимальное значение

— среднее линейное отклонение

— дисперсия (по генеральной совокупности и по выборке)

— среднее квадратическое отклонение (по генеральной совокупности и по выборке)

Факт возможности расчета упомянутых показателей в Excel свидетельствует о практическом их использовании. И, несмотря на очевидность некоторых моментов, я постараюсь расписать все подробно.

Максимальное и минимальное значение

Начнем с формул максимума и минимума. Что такое максимальное и минимальное значение, уверен, знают почти все. Максимум – самое большое значение из анализируемого набора данных, минимум – самое маленькое (может быть и отрицательным числом).

Это крайние значения в совокупности данных, обозначающие границы их вариации. Примеры реального использования каждый может придумать сам – их полно. Это и минимальные/максимальные цены на что-нибудь, и выбор наилучшего или наихудшего решения задачи, и всего, чего угодно.

Минимум и максимум – весьма информативные показатели. Давайте теперь их рассчитаем в Excel.

Выбираем нужную формулу, в следующем окошке указываем диапазон данных (в котором ищется максимальное или минимальное значение) и жмем «ОК».

Функции МАКС и МИН достаточно часто используются, поэтому разработчики Экселя предусмотрительно добавили соответствующие кнопки в ленту. Они находятся там же, где суммаи среднее значение – в разворачивающемся списке.

В общем, для вызова функции максимума или минимума действий потребуется не больше, чем для расчета средней арифметической. Все архипросто.

Среднее линейное отклонение

Среднее линейное отклонение, напоминаю, представляет собой среднее из абсолютных (по модулю) отклонений от средней арифметической в анализируемой совокупности данных. Математическая формула имеет вид:

где

a – среднее линейное отклонение,

x – анализируемый показатель, с черточкой сверху – среднее значение показателя,

n – количество значений в анализируемой совокупности данных.

В Excel эта функция называется СРОТКЛ.

После выбора функции СРОТКЛ указываем диапазон данных, по которому должен произойти расчет. Нажимаем «ОК». Наслаждаемся результатом.

Среднее квадратическое отклонение

Среднеквадратическое отклонение по генеральной совокупности – это корень из генеральной дисперсии.

Выборочное среднеквадратическое отклонение – это корень из выборочной дисперсии.

Для расчета можно извлечь корень из формул дисперсии, указанных чуть выше, но в Excel есть и готовые функции:

— Среднеквадратическое отклонение по генеральной совокупности СТАНДОТКЛОН.Г

— Среднеквадратическое отклонение по выборке СТАНДОТКЛОН.В.

С названием этого показателя может возникнуть путаница, т.к. часто можно встретить синоним «стандартное отклонение». Пугаться не нужно – смысл тот же.

Далее, как обычно, указываем нужный диапазон и нажимаем на «ОК». Среднее квадратическое отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными. Об этом ниже.

Пример XYZ анализа объемов продаж продукции в Excel

Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс

Бесплатный Экспресс-курс «Оценка инвестиционных проектов с нуля в Excel» от Ждановых. Получить доступ

Для того чтобы лучше понять смысл XYZ анализа рассмотрим реальный пример. В нашем случае есть магазин сотовых телефонов и имеются объем продаж различных марок. Для корректного применения анализа необходимо, чтобы период продаж рассмотрения был не менее 4 месяцев.

Ассортимент и объем продаж продукции

Далее необходимо рассчитать изменчивость объема продаж по каждой товарной группе. На рисунке ниже показан итог расчета коэффициента вариации  по продукции. Формула расчета в Excel будет иметь следующий вид:

Коэффициент вариации объемов продаж =СТАНДОТКЛОН(B5:G5)/СРЗНАЧ(B5:G5)

Расчет коэффициента вариации продаж товаров

Сейчас необходимо классифицировать товары в группу – «X»,»Y» или «Z». Для этого напишем формулу определяющую класс товара, и воспользуемся встроенной формулой «ЕСЛИ» в Excel. Формула будет иметь следующий вид:

Группа товара =ЕСЛИ(H5<10%;»X»;ЕСЛИ(H5<25%;»Y»;»Z»))

Группировка продукции по классам XYZ в Excel

Чтобы было наглядно видно структуру устойчивости продаж необходимо провести группировку по классам: главное меню Excel → «Данные» → «Сортировка».

XYZ анализ продаж продукции в Excel. Пример расчета

В результате мы получим следующую классификацию товаров. Телефоны «Lenovo» имеют самый устойчивый спрос, так как коэффициент вариации составляет всего 8%. То есть объем продаж в среднем по месяцам отклоняется на 8%

Компании следует уделить особое внимание складским запасам данных товаров. В группу «Y» попали довольно много различных видов продукции, компании следует оперативно отслеживать складские запасы

Товары группы «Z» продаются не регулярно,  их запасы могут быть сокращены и фирма может работать по предзаказу. XYZ анализ хорошо себя зарекомендовал на практике управления запасами и ассортиментом товаров, также его часто объединяют с ABC анализом, который позволяет провести двухкритериальную группировку товаров. Более подробно о ABC анализе вы можете узнать в моей статье: «ABC анализ продаж. Пример расчета в Excel«.

Резюме

Метод XYZ анализа позволяет прогнозировать устойчивость спроса на продукции, объемы продаж и запасов. Использование метода высвобождает дополнительные ресурсы компании и оптимизирует их бизнес-процессы.

Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс

Бесплатный Экспресс-курс «Оценка инвестиционных проектов с нуля в Excel» от Ждановых. Получить доступ

Оценка стоимости бизнеса	Финансовый анализ по МСФО	Финансовый анализ по РСБУ
Расчет NPV, IRR в Excel	Оценка акций и облигаций

Как посчитать среднеквадратичное отклонение в экселе?

В программе эксель можно посчитать среднеквадратичное отклонение двумя способами: использовать стандартные формулы или воспользоваться специальной функцией. Рассмотрим оба метода расчета и сравним их результаты.

Перед нами таблица, состоящая из двух строк и шести столбцов, на основании этих данных и будем делать расчет.

Первый способ.

Первый шаг. Рассчитаем среднее значение пяти данных показателей, для этого воспользуемся функцией СРЗНАЧ, в ячейке «В3» напишем формулу: =СРЗНАЧ(B2:F2).

Второй шаг. Рассчитаем отклонения каждого показателя от среднего, для этого в ячейке «В4» пишем формулу: =B2-$B$3, знаки доллара ставим, чтобы при копировании данной формулы на другие ячейки, параметр среднего значения всегда вычитался. Копируем соответственно данную формулу на другие ячейки.

Третий шаг. Возведем каждое отклонения от среднего в квадратный корень, для этого в ячейке «В5» пишем формулу: =B4^2, которую копируем на оставшийся диапазон ячеек (с «С5» по «F5»).

Четвертый шаг. Посчитаем сумму квадратных отклонений, для этого в ячейке «В6» напишем формулу =СУММ(B5:F5).

Пятый шаг. У нас все готово, чтобы рассчитать среднеквадратичное отклонения. Для этого нужно сумму отклонений от среднего значения в квадрате (8,8) разделить на количество опытов минус один (5-1) и от получившегося значения изъять квадратный корень. Пишем в ячейке «В8» формулу: =КОРЕНЬ((B6/(5-1))).

В итоге получили цифру равную 1,483

Второй способ.

Программа эксель позволяет избегать такого количества расчетов, а, следовательно, сэкономить время, вам просто нужно воспользоваться для расчета среднеквадратичное отклонения функцией СТАНДОТКЛОН, вы внутри неё указываете диапазон, для которого нужно сделать расчет. В ячейке «В8» пишем формулу =СТАНДОТКЛОН(B2:F2).

В итоге результаты обоих вариантов расчета среднеквадратичного отклонения совпали, а вы выбирайте метод, который наиболее подходит к вам.

Другие меры разброса

Расчет коэффициента вариации с использованием Excel

Для расчета коэффициента вариации с использованием Excel следуйте следующим шагам:

1. В Excel введите свои данные в столбец или строку.
2. Используя формулу, рассчитайте среднее значение для вашего набора данных. Например, если ваши данные находятся в столбце A, формула будет выглядеть так: =СРЗНАЧ(A:A).
3. Затем рассчитайте стандартное отклонение с помощью формулы =СТАНДОТКЛ(A:A), где A это столбец с вашими данными.
4. В конечном итоге, используя формулу, рассчитайте коэффициент вариации: =СТАНДОТКЛ(A:A)/СРЗНАЧ(A:A).
5. Чтобы представить коэффициент вариации в виде процентов, умножьте его на 100: =СТАНДОТКЛ(A:A)/СРЗНАЧ(A:A)*100.

После выполнения этих шагов, Excel рассчитает коэффициент вариации на основе ваших данных. Это позволит вам оценить уровень изменчивости ваших данных и сравнивать их с другими наборами данных.

Например, если вы рассчитали коэффициент вариации и получили значение 25%, это означает, что ваш набор данных имеет относительную степень изменчивости в размере 25%. Чем выше процент, тем выше уровень изменчивости данных.

Расчет коэффициента вариации с использованием Excel — это простой и эффективный способ анализа и сравнения различных наборов данных. Он позволяет выявить различия в уровне изменчивости и принять более обоснованные решения на основе этих результатов.