Калькулятор сочетаний

Разделы

Прежде чем мы перейдем непосредственно к формулам комбинаторики и рассмотрению задач, стоит обратить внимание на то, что комбинаторика, как и другие разделы математики, имеет свои подразделы. К ним относятся:

• перечислительная;
• структурная;
• экстремальная;
• теория Рамсея;
• вероятностная;
• топологическая;
• инфинитарная.

В первом случае речь идет об исчисляющей комбинаторике, задачи рассматривают перечисление или подсчет разных конфигураций, которые образованы элементами множеств. На данные множества, как правило, накладываются какие-либо ограничения (различимость, неразличимость, возможность повтора и так далее). А количество этих конфигураций подсчитывается при помощи правила сложения или умножения, о которых мы поговорим немного позже. К структурной комбинаторике относятся теории графов и матроидов. Пример задачи экстремальной комбинаторики — какова наибольшая размерность графа, который удовлетворяет следующим свойствам… В четвертом пункте мы упомянули теорию Рамсея, которая изучает в случайных конфигурациях наличие регулярных структур. Вероятностная комбинаторика способна нам ответить на вопрос — какова вероятность того, что у заданного множества присутствует определенное свойство. Как нетрудно догадаться, топологическая комбинаторика применяет методы в топологии. И, наконец, седьмой пункт — инфинитарная комбинаторика изучает применение методов комбинаторики к бесконечным множествам.

Комбинаторные конфигурации

Рассматривая вопрос основных понятий и формул комбинаторики, мы не можем не уделить внимание комбинаторным конфигурациям. Они используются не только для формулировки, но и для решения различных Примерами таких моделей служат:

• размещение;
• перестановка;
• сочетание;
• композиция числа;
• разбиение числа.

О первых трех мы поговорим более подробно далее, а вот композиции и разбиению мы уделим внимание в данном разделе. Когда говорят о композиции некого числа (допустим, а), то подразумевают представление числа а в виде упорядоченной суммы неких положительных чисел

А разбиение — это неупорядоченная сумма.

Сколько комбинаций в нотах

Существует шесть миллиардов комбинаций, из которых композитор имеет возможность выбрать такие, которые будут мелодичны. Но это — еще не все. Ведь ноты бывают разной длительности, и ритм совершенно меняет лицо мелодии. Кроме того гармония, подголоски, аккомпанемент тоже придают мелодии совершенно иной характер.

15.04.2023 Сколько вариантов у 6 значного кода

Когда речь идет о создании паролей или кодов, важно знать, сколько возможных вариантов существует для заданной длины и набора символов. Например, если мы рассматриваем 6-значные коды, составленные из цифр, то общее количество возможных комбинаций можно определить по формуле N = 6!, что равно 720

Это означает, что при попытке угадать код с первой попытки вероятность составляет всего около 0,14%.

Однако, если мы говорим о паролях, которые могут состоять из букв и цифр, то количество возможных комбинаций значительно выше. Например, для пароля длиной 6 символов, состоящего из цифр и букв, общее количество возможных комбинаций можно определить по формуле N = m^k, где m — количество разрешенных символов для каждого знака пароля, а k — длина пароля. Если мы используем 36 возможных символов (цифры и буквы латинского алфавита), то общее количество возможных комбинаций составляет 2,2 миллиарда.

Если рассматривать конкретный набор символов, то, например, для пароля из 6 букв латинского алфавита общее количество возможных комбинаций равно 26^6, что составляет более 300 миллионов вариантов.

Если же мы говорим о заданном наборе символов, то количество возможных комбинаций также зависит от их количества и длины. Например, если нам нужно составить 6-значные коды из цифр 4, 5, 6, 7, 8 и 9, то общее количество возможных комбинаций можно определить по формуле N = m!, где m — количество символов. В данном случае количество возможных комбинаций равно 6, что означает, что мы можем составить всего 6 различных 6-значных кодов.

Кроме того, при создании паролей и кодов важно учитывать вероятность их угадывания. Например, существует статистика распространенных паролей и кодов, которые часто используются людьми и которые легко угадываются злоумышленниками

Наиболее популярными четырехзначными паролями являются 1234, 0000, 2580, 1111, 5555, 5683, 0852, 2222, 1212 и 1998, а шестизначными — 123456, 654321, 111111, 000000, 123123, 666666, 121212, 112233, 789456 и 159753.

Таким образом, при создании паролей и кодов важно учитывать все возможные варианты, а также вероятность их угадывания. Важно использовать сложные пароли, включающие различные символы, и не использовать распространенные и легкоузнаваемые коды

Основная формула комбинаторики

Пусть имеется k групп элементов, причем i-я группа состоит из n i элементов.
Выберем по одному элементу из каждой группы. Тогда общее число N способов,
которыми можно произвести такой выбор, определяется соотношением N=n 1 *n 2 *n 3 *…*n k .

Пример 1.
Поясним это правило на простом
примере. Пусть имеется две группы элементов, причем первая группа состоит из
n 1 элементов, а вторая — из n 2 элементов. Сколько
различных пар элементов можно составить из этих двух групп, таким образом,
чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли
первый элемент из первой группы и, не меняя его, перебрали все возможные
пары, меняя только элементы из второй группы. Таких пар для этого элемента
можно составить n 2 . Затем мы берем второй элемент из первой группы
и также составляем для него все возможные пары. Таких пар тоже будет n 2 .
Так как в первой группе всего n 1 элемент, всего возможных
вариантов будет n 1 *n 2 .

Пример 2.
Сколько
трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если
цифры могут повторяться?Решение:
n 1 =6
(т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n 2 =7
(т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5,
6), n 3 =4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4,
6).
Итак, N=n 1 *n 2 *n 3 =6*7*4=168.

В том случае, когда все группы состоят из одинакового числа элементов, т.е. n 1 =n 2 =…n k =n
можно считать, что каждый выбор производится из одной и той же группы, причем
элемент после выбора снова возвращается в группу. Тогда число всех способов
выбора равно n k . Такой способ выбора в комбинаторики носит название выборки с возвращением.

Пример 3.
Сколько всех четырехзначных чисел
можно составить из цифр 1, 5, 6, 7, 8?Решение.
Для каждого разряда
четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=5 4 =625.

Рассмотрим множество, состоящие из n элементов. Это
множество в комбинаторике называется генеральной
совокупностью
.

Сколько комбинаций можно составить из 8 цифр

N = m ^ k, где N — количество возможных комбинаций, m — количество разрешенных символов для каждого знака пароля, k — длина пароля. Следовательно, количество возможных паролей, состоящих из 8 символов, составит: N = 92 ^ 8 = 5 132 188 731 375 616 = 5,1 * 10 ^ 15.

09.04.2023 Сколько комбинаций можно составить из 4 цифр

Когда речь идет о комбинациях из цифр, первым делом нужно понимать, сколько всего возможных вариантов существует. Если рассматривать комбинации из 4 цифр, то выходит, что их может быть 10 000. Это значит, что каждая из цифр от 0 до 9 может быть представлена в каждом из четырех знаков.

Однако, если мы ограничиваемся цифрами 1, 2, 3 и 4, то ситуация меняется. Теперь мы имеем всего 4 возможных варианта для каждого из четырех знаков. Таким образом, общее количество комбинаций определяется по формуле 4! (четыре факториала), что равно 24.

Но как на практике определить вероятность угадать пароль из 4 цифр? Если мы предположим, что пин-код выбирается случайным образом, то вероятность угадать пароль состоящий из четырех одинаковых цифр будет равна 0,001 (или 10 на 10 000). Но что насчет других возможных комбинаций? Какие пароли из 4 цифр могут быть наиболее распространенными?

Исследования показали, что наиболее часто используемыми четырехзначными паролями являются 1234, 0000, 2580, 1111, 5555, 5683, 0852, 2222, 1212 и 1998. Шестизначными же паролями, которые часто используются, оказались 123456, 654321, 111111, 000000, 123123, 666666, 121212, 112233, 789456 и 159753.

Если рассматривать комбинации из 3 цифр, не допуская повторений, то можно заметить, что таких комбинаций всего 6. Например, это могут быть комбинации 123, 132, 213, 231, 312 и 321.

Если же мы говорим о комбинациях из 3 цифр без ограничений на повторение, то тут уже можно применить формулу для расчета количества возможных комбинаций. Если рассматривать комбинации из цифр от 1 до 9, то получится, что для каждого из трех знаков существует 9 возможных вариантов. Таким образом, всего получается 9*9*9 = 729 комбинаций.

Наконец, если мы рассматриваем комбинации из 6 цифр с возможностью повторений, то существует 720 возможных вариантов. Такой результат получается, если применить формулу N!, где N — количество цифр, а восклицательный знак обозначает факториал.

В целом, для расчета количества возможных комбинаций пароля нужно использовать формулу N = m^k, где N — количество возможных комбинаций, m — количество разрешенных символов для каждого знака пароля, а k — длина пароля.

Таким образом, при работе с комбинациями цифр нам необходимо учитывать ограничения на возможные символы, а также на повторение их в пароле

Важно понимать, что количество возможных комбинаций напрямую влияет на безопасность пароля, поэтому при выборе пароля стоит учитывать этот фактор

Перестановка

Сейчас мы рассмотрим еще одну формулу комбинаторики. В данном разделе статьи мы поговорим о перестановках. Рассмотреть проблему предлагаем сразу же на примере. Возьмем бильярдные шары у нас их n-ое количество. Нам нужно подсчитать: сколько есть вариантов расставить их в ряд, то есть составить упорядоченный набор.

Начнем, если у нас нет шаров, то и вариантов расстановки у нас так же ноль. А если у нас шар один, то и расстановка тоже одна (математически это можно записать следующим образом: Р1 = 1). Два шара можно расставить двумя разными способами: 1,2 и 2,1. Следовательно, Р2 = 2. Три шара можно расставить уже шестью способами (Р3=6): 1,2,3; 1,3,2; 2,1,3; 2,3,1; 3,2,1; 3,1,2. А если таких шаров не три, а десять или пятнадцать? Перечислять все возможные варианты очень долго, тогда нам на помощь приходит комбинаторика. Формула перестановки поможет нам найти ответ на интересующий нас вопрос. Pn = n *P (n-1). Если попытаться упростить формулу, то получаем: Pn = n* (n — 1) *…* 2 * 1. А это и есть произведение первых натуральных чисел. Такое число называется факториалом, а обозначается как n!

Рассмотрим задачу. Вожатый каждое утро выстраивает свой отряд в шеренгу (двадцать человек). В отряде есть три лучших друга — Костя, Саша и Леша. Какова вероятность того, что они будут стоять рядом? Чтобы найти ответ на вопрос, нужно вероятность «хорошего» исхода поделить на общее количество исходов. Общее число перестановок составляет 20! = 2,5 квинтиллиона. Как посчитать количество «хороших» исходов? Предположим, что Костя, Саши и Леша — это один сверхчеловек. Тогда мы имеем всего восемнадцать субъектов. Число перестановок в данном случае равняется 18 = 6,5 квадриллионов. При всем этом, Костя, Саша и Леша могут произвольно перемещаться между собой в своей неделимой тройке, а это еще 3! = 6 вариантов. Значит всего «хороших» расстановок у нас 18! * 3! Нам остается только найти искомую вероятность: (18! * 3!) / 20! Что равняется примерно 0,016. Если перевести в проценты, то это получается всего 1,6%.

Сочетания без повторений

Сочетанием без
повторения из
n


элементов по
m


называется любое неупорядоченное
подмножество множества
N
,
содержащее
m


различных элементов.

Из определения
следует, что два сочетания различаются
только элементами, порядок не важен.

Теорема 5
.
Число сочетаний без повторений вычисляют
по одной из следующих формул:

Пример 1
.
В комнате 5 стульев. Сколькими способами
можно разместить на них

а) 7 человек; б) 5
человек; в) 3 человека?

Решение:

а) Прежде всего надо выбрать 5 человек
из 7 для посадки на стулья. Это можно
сделать
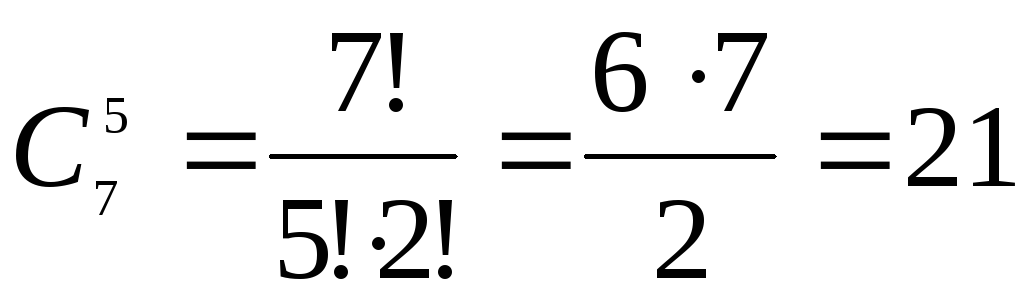способом. С каждым выбором конкретной
пятерки можно произвести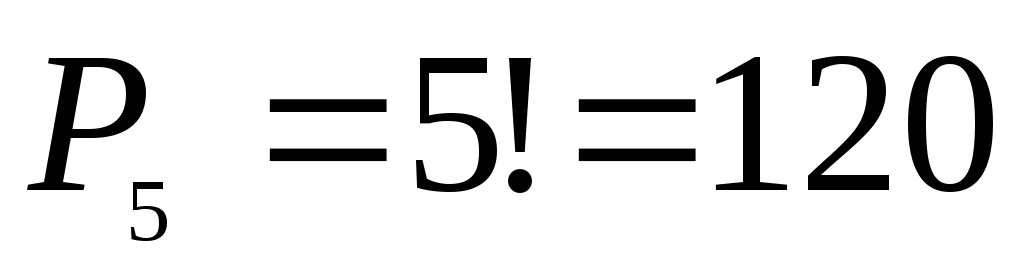перестановок местами. Согласно теореме
умножения искомое число способов посадки
равно.

Замечание:

Задачу можно решать, используя только
теорему произведения, рассуждая следующим
образом: для посадки на 1-й стул имеется
7 вариантов, на 2-й стул-6 вариантов, на
3-й -5, на 4-й -4 и на 5-й -3. Тогда число способов
посадки 7 человек на 5 стульев равно
.
Решения обоими способами согласуются,
так как

б) Решение очевидно
—

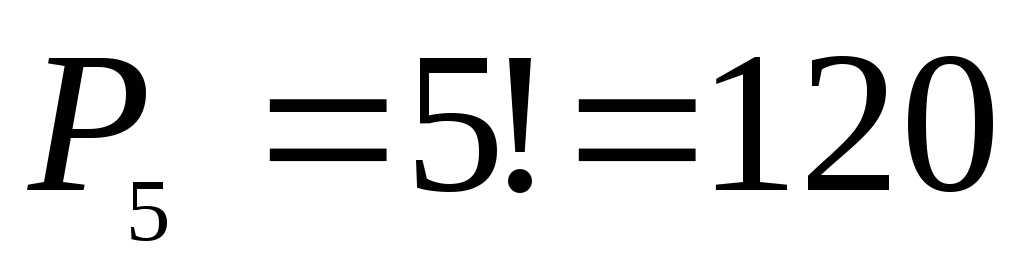
в)
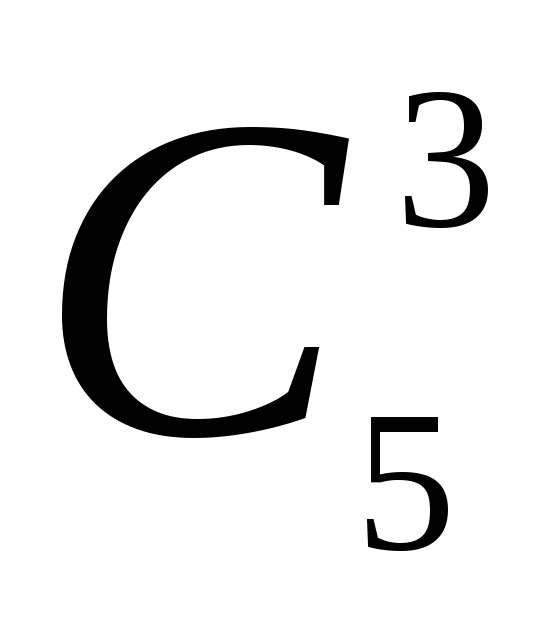— число выборов занимаемых стульев.

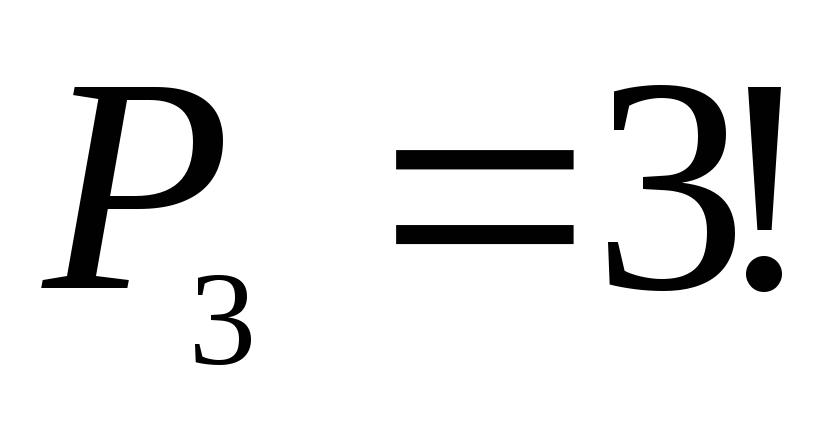— число размещений
трех человек на трех выбранных стульях.

Общее число выборов
равно
.

Не трудно проверить
формулы
;

;

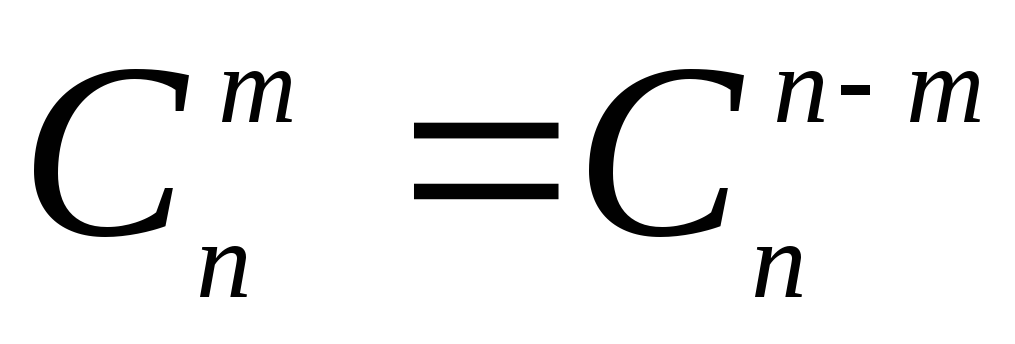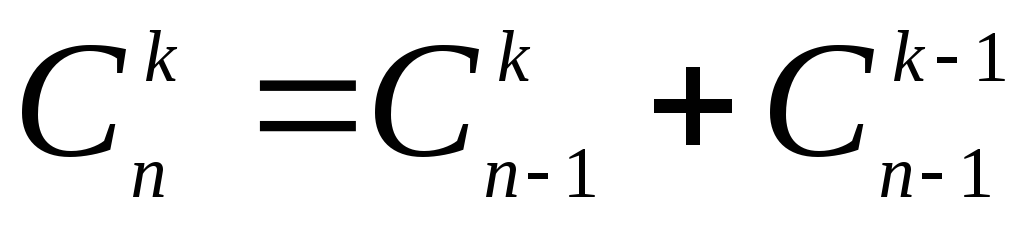Число всех подмножеств множества,
состоящего из n

элементов.

Как использовать количество комбинаций в реальной жизни?

1. Игры и головоломки.

Количество комбинаций может быть использовано для создания игр и головоломок, в которых необходимо найти все возможные варианты. Например, если у вас есть комбинационный замок, вы можете использовать количество комбинаций для определения количества возможных кодов, которые можно установить.

2. Заказ товаров и услуг.

Количество комбинаций может помочь в организации процессов заказа товаров или услуг. Например, если у вас есть 5 разных товаров, и вы хотите выбрать 3 из них, количество комбинаций позволит определить количество вариантов выбора.

3. Шифрование и безопасность.

Количество комбинаций может быть использовано для создания сложных паролей и кодов, повышающих безопасность. Чем больше комбинаций возможно создать, тем сложнее их угадать или взломать.

4. Маркетинг и исследования.

Количество комбинаций может быть полезно в маркетинге и исследованиях, помогая оценить различные варианты и возможности. Например, при проведении опроса или эксперимента количество комбинаций позволяет определить группы, которые можно сформировать для анализа.

В конечном итоге, количество комбинаций используется для описания и оценки разнообразия и возможностей в различных ситуациях. Оно помогает облегчить процессы принятия решений и позволяет найти оптимальные варианты.

Фундаментальный принцип расчета

Фундаментальный принцип счета помогает нам найти количество способов выполнения различных задач. Существуют два фундаментальных правила счета.

Правило суммы

Если первая задача может быть выполнена m способов, вторая задача может быть выполнена n способов, и если задачи не могут быть выполнены одновременно, то выполнение любой из этих задач может быть выполнено количеством способов равным (m + n).

Правило произведения

Если первая задача может быть выполнена m способами, а вторая задача может быть выполнена n способами и обе задачи могут быть выполнены одновременно, то существует (m × n) способов выполнения обеих задач одновременно.

Примеры

Предположим, вы хотите подсчитать количество способов подбросить монету и бросить кубик. Поскольку у монеты две грани, количество способов бросить монету равно 2. Аналогично, есть 6 возможных способов бросить кубик. Поскольку вы можете выполнять обе задачи одновременно, есть 2 × 6 = 12 способов подбросить монету и бросить кубик.

Если вы хотите взять 2 карты из колоды в 52 карты без возвращения ее на место, есть 52 способа взять первую карту и 51 способ взять вторую. Следовательно, количество способов вытянуть две карты равно 52 × 51 = 2.652.

Как использовать онлайн-калькулятор сочетаний:

Онлайн-калькулятор комбинаций чисел требует различных значений для точного расчета, это шаги, которые вы должны выполнить, чтобы получить мгновенные результаты.

Входы:

• Прежде всего, выберите имя элементов набора данных из раскрывающегося списка этого инструмента.
• Затем введите общее количество элементов в предназначенное для этого поле.
• Затем введите, сколько элементов вы хотите выбрать из общего числа элементов.
• Затем вам нужно выбрать, что вы хотите создать, из раскрывающегося меню. Это может быть как комбинация, так и комбинация с повторением.
• Затем вставьте значения элементов в указанное поле.
• Наконец, нажмите кнопку “Рассчитать”.

Выходы:

Как только вы закончите, калькулятор формулы комбинации покажет:

• Комбинация
• Сочетание с повторением
• Пошаговый расчет

Заметка:

Не беспокойтесь, хотите ли вы получить расчет с комбинацией или повторением, все, что вам нужно, чтобы выбрать соответствующую опцию, калькулятор комбинации покажет вам результат в соответствии с заданными значениями.

Как рассчитать выигрышную комбинацию 5 из 36

Развернутая система – в погоне за 100% выигрышем джекпота

100% шанс на выигрыш в лотерею даст только развернутая система, в которую будут входить все 36 чисел, то есть ставка на все возможные комбинации. Однако такую ставку будет сделать не возможно и не разумно по нескольким причинам:

1. Ограничения по правилам. Количество выбранных чисел в развернутой ставке согласно правилам лотереи не превышает 11, оформить такую ставку в которой в одном билете будут зачеркнуты все числа нельзя.

2. Предположим, что кто-то вручную или автоматически всё же решится скупить все возможные комбинации на предстоящий тираж.

Такая ставка была бы вполне реализуема, если была бы логична её экономическая составляющая. Джекпот Гослото 5 из 36 никогда даже близко не подбирался к этой сумме, и никогда не подберется к этой сумме даже близко. Выигрыш джекпота при такой ставке конечно будет с вероятностью 100%, но сумма выигрыша по нему не покроет сумму необходимую потратить на покупку такого количества билетов.

Четыре развернутые системы – в погоне за выигрышем.

Все 36 чисел лотереи можно разложить поровну в четыре мешочка.

В каждом мешочке будет по 9 чисел. Всего же в ходе розыгрыша выпадает пять чисел.

Соответственно, если первые четыре выпавших чисел окажутся в разных мешочках, то пятое число окажется в одном из мешочков, в котором уже есть выпавшее число. То есть как ни крути при самом плохом варианте один из мешочков будет содержать 2 выигрышных числа, то есть окажется выигрышным.

Стоимость четырех таких ставок при сумме билета в 80 рублей будет равняться 40 320 рублям при гарантированном выигрыше равном 80 рублей.

Казалось бы, экономическая целесообразность такой ставки также сомнительна, но не надо забывать, что такая ставка может сорвать и приз более крупной категории, но здесь уже без каких либо 100% гарантий.

Так, вероятность совпадения трех чисел в такой ставке будет менее 30%, а вероятность выигрыша джекпота будет равна стандартной вероятности, как при покупке 504 билетов со случайными комбинациями.

Еще несколько систем игры в Гослото 5 из 36

Наша программа под названием Нострадамус пытается угадать выигрышную комбинацию ближайшего тиража на основе статистического анализа и других факторов, формируя лишь одну комбинацию.

Неполные системы 5 из 36 являются более щадящим по финансам аналогом развернутых систем. Многие игроки находят эту систему основной для своей игры.

Сбалансированная стратегия подвергает элементарному математическому анализу выпавшие комбинации.

Вывод

Лотерея остается лотереей – азартным увлечением, приносящее немногочисленным победителям миллионые выигрышы. В статье рассмотрены некоторые возможные методики выигрыша и теория вероятности в лотерее Гослото 5 из 36.

Система выигрыша в лотерею от многократного победителя

Конечное примечание:

К счастью, вы узнали, что комбинации используются для определения возможных расположений в коллекции n элементов. Когда дело доходит до вычисления большого числа, воспользуйтесь бесплатным онлайн-калькулятор сочетаний, который поможет вам найти комбинацию данных элементов.

Other Languages: Combination Calculator, Kombinasyon Hesaplama, Kalkulator Kombinacji, Kalkulator Kombinasi, Kombinatorik Rechner, 組み合わせ 計算, 조합 계산기, Kombinace Kalkulačka, Calculadora De Combinações, Calcul Combinaison, Calculadora De Combinaciones, Calcolo Combinatorio, Yhdistelmää Laskin, Kombinations Beregner, Kombinatorikk Kalkulator.