Как подсчитать количество паролей, которые удовлетворяют следующим требованиям? [закрыт]
Закрыт. Этот вопрос не по теме. Ответы на него в данный момент не принимаются.
Учебные задания допустимы в качестве вопросов только при условии, что вы пытались решить их самостоятельно перед тем, как задать вопрос. Пожалуйста, отредактируйте вопрос и укажите, что именно вызвало у вас трудности при решении задачи. Например, приведите код, который вы написали, пытаясь решить задачу
Закрыт 2 года назад .
Паролем должны содержать от 3 до 5 символов, среди которых должно быть хотя бы 2 различных, а символами пароля могут быть только десятичные цифры 0-9 и строчные буквы a-z. Сколько паролей удовлетворяют перечисленным требованиям?
Прямое произведение
Прямое, или декартово произведение двух множеств — множество, элементами которого являются все возможные упорядоченные пары элементов исходных множеств. Проще говоря мы берем из первого множества один элемент, а потом из второго выбираем элемент и составляем их в кортеж. Так вот все способы выбрать так элементы – составят декартово произведение. Пример:
>>> A = >>> B = "123" >>> print(*product(A, B)) (1, 'a') (1, 'b') (1, 'c') (2, 'a') (2, 'b') (2, 'c') (3, 'a') (3, 'b') (3, 'c')
Примечания. Во-первых, заметьте, что элементы следуют в строгом лексографическом порядке: сначала берется нулевой элемент из первой последовательности и сочетается с каждым по очереди из второй последовательности. Во-вторых, аргументами функции могут быть любые итерируемые объекты конечной длины. Я взял для примера список и строку, причем строка автоматически разбивается на символы.
В коде произведение множеств эквивалентно вложенным циклам:
>>> print(*) (1, '1') (1, '2') (1, '3') (2, '1') (2, '2') (2, '3') (3, '1') (3, '2') (3, '3')
Результат такой же, но рекомендую использовать именно библиотечную функцию, так как ее реализация, наверняка, будет лучше.
Вы можете передать в функцию больше последовательностей:
>>> print(*product()) (1,) (2,) (3,) >>> print(*product(, )) (1, 10) (1, 20) (1, 30) (2, 10) (2, 20) (2, 30) (3, 10) (3, 20) (3, 30) >>> print(*product(, , )) (1, 10, 100) (1, 10, 200) (1, 10, 300) (1, 20, 100) (1, 20, 200) (1, 20, 300) (1, 30, 100) (1, 30, 200) (1, 30, 300) (2, 10, 100) (2, 10, 200) (2, 10, 300) (2, 20, 100) (2, 20, 200) (2, 20, 300) (2, 30, 100) (2, 30, 200) (2, 30, 300) (3, 10, 100) (3, 10, 200) (3, 10, 300) (3, 20, 100) (3, 20, 200) (3, 20, 300) (3, 30, 100) (3, 30, 200) (3, 30, 300)
Каждый выходной элемент будет кортежем (даже в случае, если в нем только один элемент!)
Также обратите внимание на то, что функция product (как и все остальные из сегодняшнего набора) возвращает не список, а особый ленивый объект. Чтобы получить все элементы, нужно преобразовать его в список функцией list:
>>> product(, 'abc') <itertools.product object at 0x101aef8c0> >>> list(product(, 'abc'))
Количество элементов на выходе будет произведением длин всех последовательностей на входе:
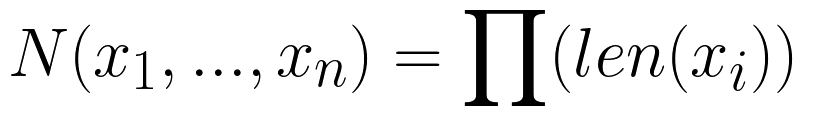
В функцию product можно передать именованный параметр repeat, который указывает сколько раз повторять цепочку вложенных циклов (по умолчанию один раз). Если repeat >= 2, то это называют декартовой степенью. То есть множество умножается на себя несколько раз. Так при repeat=2 эквивалентным кодом будет:
>>> == list(product(A, B, repeat=2)) True
В таком случае количество элементов в результате будет вычисляться по схожей формуле с учетом того, что каждый множитель будет в степени repeat:
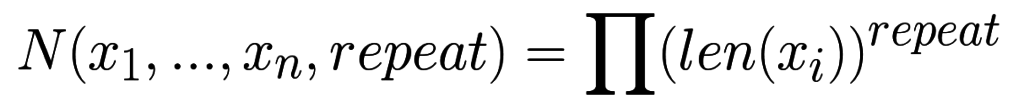
Ноль — это действительное число?
На самом деле настоящие числа — это практически любые числа, которые вы можете придумать. … Действительные числа могут быть положительными или отрицательными, и включить число ноль. Их называют действительными числами, потому что они не являются мнимыми, а это другая система чисел.
Пи действительное число? Вкратце, пи, которое записывается как греческая буква р или π, представляет собой отношение длины окружности любого круга к диаметру этого круга. … Цель пи — иррациональное число, что означает, что его десятичные формы не заканчиваются (например, 1/4 = 0.25) и не повторяются (например, 1/6 = 0.166666…).
Что такое R * в математике?
В математике обозначение R * представляет два разных значения. В системе счисления R * определяет набор всех ненулевых действительных чисел, который образует группу по операции умножения. В функциях R* определяет рефлексивно-транзитивное замыкание бинарного отношения «R» в множестве. 4 (4)
Для чего придумали факториал? Использование! был основан Кристианом Крампом в 1808 г.. Хотя они могут показаться очень простыми, использование факториальной записи для неотрицательных целых чисел и дробей немного сложно. Приложения варьируются от простой алгебры до исчисления, и он также используется для определения вероятностей.
Что такое заглавная гамма в математике?
В математике гамма-функция (обозначаемая буквой Γ, заглавной буквой гамма из греческого алфавита) является одним из часто используемых расширений функции гаммы. факториальная функция комплексных чисел. Гамма-функция определена для всех комплексных чисел, кроме неположительных целых чисел.
Как расширить N?
Алгоритм
Единственное, что нам понадобится нового для рекурсии, о чём мы ещё не говорили, — это мемоизация.
В программировании мемоизацией называют временное хранение промежуточных результатов вычислений, чтобы не вычислять их по сто раз. Один раз посчитал, добавил в переменную-кеш — и отлично.
В нашем случае за это будет отвечать такая строчка:
Она появляется в самом начале рекурсии и означает вот что:
- Если в переменной memo уже что-то было — используется то, что было.
- Если на момент запуска рекурсии в этой переменной ничего не было — создаётся пустой массив.
Так мы избавляемся от необходимости высчитывать промежуточные последовательности заново, а вместо этого используем временное хранилище.
Теперь смотрите код и читайте комментарии:
Запустим код в консоли браузера:

Видно, что мы получили 24 перестановки, как и должно было быть. Они все разные, ни в одной нет повторений — то, что нам нужно. Теперь можно отдать эти последовательности дальше, чтобы по каждой из них собрали своё письмо для клиентов.
Если интересно, как рекурсия справится со сложными вариантами и сколько их получится, — сделайте в исходном массиве в коде не 4, а 10 элементов.
Примеры трехзначных комбинаций
Трехзначные комбинации — это числа, состоящие из трех цифр, которые могут принимать значения от 100 до 999. Всего возможно 900 различных комбинаций трехзначных чисел. Ниже приведены некоторые примеры таких комбинаций:
Пример 1:
Число 123 является трехзначной комбинацией, которая состоит из цифр 1, 2 и 3. Оно находится между числами 100 и 999 и обладает своей уникальной числовой ценностью. Каждая цифра в этой комбинации представляет определенное значение: 1 — сотни, 2 — десятки и 3 — единицы.
Пример 2:
Число 789 представляет собой трехзначную комбинацию, состоящую из цифр 7, 8 и 9. Оно находится между числами 100 и 999 и имеет свою собственную числовую величину. Каждая из цифр в этой комбинации имеет свое значение: 7 — сотни, 8 — десятки и 9 — единицы.
Пример 3:
Число 555 является трехзначной комбинацией, которая состоит из трех цифр 5. Оно находится между числами 100 и 999 и обладает своей уникальной числовой ценностью. Каждая цифра в этой комбинации представляет определенное значение: 5 — сотни, 5 — десятки и 5 — единицы.
Таким образом, существует множество трехзначных комбинаций, каждая из которых имеет свою уникальную числовую ценность и представляет определенные значения для каждой цифры. Эти комбинации могут быть использованы в различных математических операциях, а также в задачах, требующих учета различных вариаций чисел
Важно помнить, что трехзначные комбинации необходимо обрабатывать с учетом их уникальности и собственных числовых величин
Примеры трехзначных комбинаций
Трехзначные комбинации — это числа, состоящие из трех цифр, которые могут принимать значения от 100 до 999. Всего возможно 900 различных комбинаций трехзначных чисел. Ниже приведены некоторые примеры таких комбинаций:
Пример 1:
Число 123 является трехзначной комбинацией, которая состоит из цифр 1, 2 и 3. Оно находится между числами 100 и 999 и обладает своей уникальной числовой ценностью. Каждая цифра в этой комбинации представляет определенное значение: 1 — сотни, 2 — десятки и 3 — единицы.
Пример 2:
Число 789 представляет собой трехзначную комбинацию, состоящую из цифр 7, 8 и 9. Оно находится между числами 100 и 999 и имеет свою собственную числовую величину. Каждая из цифр в этой комбинации имеет свое значение: 7 — сотни, 8 — десятки и 9 — единицы.
Пример 3:
Число 555 является трехзначной комбинацией, которая состоит из трех цифр 5. Оно находится между числами 100 и 999 и обладает своей уникальной числовой ценностью. Каждая цифра в этой комбинации представляет определенное значение: 5 — сотни, 5 — десятки и 5 — единицы.
Таким образом, существует множество трехзначных комбинаций, каждая из которых имеет свою уникальную числовую ценность и представляет определенные значения для каждой цифры. Эти комбинации могут быть использованы в различных математических операциях, а также в задачах, требующих учета различных вариаций чисел
Важно помнить, что трехзначные комбинации необходимо обрабатывать с учетом их уникальности и собственных числовых величин
Сколько вариантов цифр в трёхзначном коде?
Многие люди задаются вопросом: сколько всего вариантов можно составить из трёхзначного кода? Этот вопрос имеет отношение к таким областям, как криптография, информационная безопасность, а также математика и статистика. Цифровой код – это набор символов или чисел, которые составляют определенную систему, в которой каждый символ имеет свое значение. Это может быть комбинация из цифр от 0 до 9, букв алфавита или специальных символов. В случае трёхзначного кода мы имеем дело только с цифрами от 0 до 9.
Для определения количества вариантов трёхзначного кода можно использовать принцип умножения. Каждая позиция в коде, начиная с самой левой, имеет 10 возможных значений (цифр от 0 до 9). Таким образом, первая позиция может принимать одно из 10 значений, вторая позиция – ещё одно из 10 значений, а третья позиция также – одно из 10 значений. Для определения общего количества вариантов нужно перемножить все эти значения: 10 × 10 × 10 = 1000.
Таким образом, в трёхзначном коде можно составить 1000 различных вариантов. Это означает, что каждое трёхзначное число от 000 до 999 может быть использовано в десятичной системе для кодирования или представления информации. Код может быть использован для идентификации, шифрования информации или в других целях.
Примеры расчета количества комбинаций
Рассмотрим несколько примеров, чтобы лучше понять, как расчитывается количество комбинаций из трех цифр:
1. Пусть у нас есть три различные цифры: 1, 2, 3. Мы можем выбрать любую из этих цифр в качестве первой цифры в комбинации, затем любую из оставшихся двух цифр в качестве второй цифры, и оставшуюся цифру в качестве последней цифры. Таким образом, у нас будет 3 возможных варианта.
2. Теперь предположим, что у нас есть три одинаковые цифры: 5, 5, 5. В этом случае мы можем выбрать любую из этих цифр в качестве первой, второй и третьей цифры в комбинации. Таким образом, у нас будет только 1 вариант комбинации.
3. Усложним задачу и рассмотрим случай, когда у нас есть три цифры, но две из них повторяются, а третья отличается: 2, 2, 8. В этом случае мы можем выбрать любую из двух цифр «2» в качестве первой и второй цифры комбинации, а третьей цифрой будет «8». Таким образом, у нас будет 2 возможных варианта комбинаций.
4. Наконец, рассмотрим случай, когда у нас есть три повторяющиеся цифры: 9, 9, 9. В этом случае у нас имеется только одна цифра для выбора всех трех цифр комбинации, поэтому у нас будет всего 1 вариант комбинации.
Размещения, сочетания и перестановки из трёх элементов
Представьте себе, что вы забыли пароль входа в аккаунт. Помните только, что это было трёхзначное число из цифр 1,2,3 и эти цифры не повторялись. Есть ли у вас шансы с помощью перебора зайти в аккаунт, если даётся всего три попытки? Такие задачи в современной жизни возникают довольно часто, и их решения изучаются в особом разделе математики — комбинаторике.
Комбинаторика – раздел математики, изучающий различные комбинации, которые можно составить из дискретных объектов, входящих в некоторое множество.
«Дискретные объекты» — это какие-то предметы, растения, животные, люди, здания, числа; всё, что можно «отделить» («дискретный» означает «отдельный») . Множество подобных объектов – это какая-то конечная группа, выбранная по какому-нибудь признаку.
Количество комбинаций из трех чисел
Думаю у многих есть дома чемодан и на этом чемодане есть замок с 3 дисками на каждом по 9 цифр.Ну так вот подскажите пожалуйста скока комбинаций можно составить из этих цифр?
Дополнен 14 лет назад
Извиняюсь не 9,а 10 цифр на каждом диске!Лучший ответ
Вопрос — сколько существует трехзначных чисел с различными цифрами? Ответ: произвольный набор способов вычисляется по правилам произведения: k1*k2. *kN 10*10*10=1000 комбинаций
Мы постоянно добавляем новый функционал в основной интерфейс проекта. К сожалению, старые браузеры не в состоянии качественно работать с современными программными продуктами. Для корректной работы используйте последние версии браузеров Chrome, Mozilla Firefox, Opera, Microsoft Edge или установите браузер Atom.
Практическое применение комбинаций из 3 чисел
Комбинации из 3 чисел от 0 до 9 могут быть полезны во множестве практических ситуаций. Вот некоторые примеры, где вы можете использовать эти комбинации:
- Пароли и коды доступа: Если вы ищете возможные пароли или коды доступа, комбинации из 3 чисел могут помочь вам сгенерировать все возможные варианты, которые могут быть использованы в защищенных системах.
- Анализ данных: Если у вас есть набор данных, содержащих числовые значения, вы можете использовать комбинации из 3 чисел для создания различных групп или категорий для анализа.
- Игры: Многие игры, как классические настольные игры, так и компьютерные, используют комбинации чисел как часть геймплея. Вы можете использовать комбинации из 3 чисел для создания возможных вариантов ходов или стратегий в играх.
- Маркетинг: Комбинации из 3 чисел также могут быть использованы в маркетинге. Например, вы можете использовать эти комбинации для создания уникальных кодов скидок или предложений для ваших клиентов.
Это лишь несколько примеров того, как комбинации из 3 чисел могут быть полезны в реальной жизни. Рассмотрите свою конкретную ситуацию и вы сможете найти свое собственное практическое применение этим комбинациям.
1. Всего существует 10 * 10 * 10 = 1000 различных комбинаций из 3 чисел от 0 до 9.
2. Каждая комбинация состоит из трех чисел, которые могут повторяться или быть одинаковыми.
3. Первое число в комбинации может принимать любое значение от 0 до 9.
4. Второе число в комбинации также может принимать любое значение от 0 до 9.
5. Третье число в комбинации также может принимать любое значение от 0 до 9.
6. Некоторые комбинации могут быть одинаковыми, например, (1, 2, 3) и (3, 2, 1) считаются одной и той же комбинацией.
7. Для каждой комбинации можно вычислить сумму, произведение и другие математические операции.
8. При исследовании комбинаций можно рассмотреть различные аспекты, такие как перестановки и сочетания.
Изучение комбинаций из 3 чисел от 0 до 9 позволяет развивать навыки анализа и решения задач, а также может применяться в различных областях, таких как математика, игры, шифрование и другие.
Сколько вариантов пароля в 4 значном коде
Количество комбинаций можно посчитать по формуле I^n, где n — количество позиций, а I — количество цифр, букв в одной позиции. 10^3=1000. Ваш кодовый замок имеет 1000 комбинаций паролей.
Сколько может быть вариаций 4 значного пароля
Рассмотрим, скольео всего можно составить комбинаций из 4 цифр. Поскольку на каждое из 4 мест можно поставить любую цифру из десяти, то возможных комбинаций будет 10*10*10*10=10^4=10000.
Сколько может быть 4 значных пароля
Четырехзначный PIN-код можно использовать для создания 10 тыс. различных комбинаций, а шестизначный — для создания 1 млн. Однако пользователи предпочитают определенные наборы чисел и используют их намного чаще, например, 123456 и 654321, — пояснили эксперты.
Почему пин код сократили до 4 цифр
Изобретатель пин-кода сократил его до 4 цифр, потому что его жена не могла запомнить больше — Во-первых, Джон с трудом причесывался самостоятельно. — Во-вторых, Джон, вообще говоря, был подкаблучник. Он быстро подсчитал в уме, что из четырех цифр можно собрать всего 10 тысяч комбинаций и это, мягко сказать, маловато.
Какие бывают 4 значные пароли
Наиболее распространенными четырехзначными PIN-кодами оказались 1234, 0000, 2580, 1111, 5555, 5683, 0852, 2222, 1212 и 1998, а шестизначными — 123456, 654321, 111111, 000000, 123123, 666666, 121212, 112233, 789456 и 159753.
27.05.2023 Сколько вариантов пароля в 4 значном коде
При использовании 4-значного кода можно создать 10 тыс. различных комбинаций, включая все числа от 0000 до 9999. Это огромное количество вариантов, но стоит отметить, что некоторые из них использовались гораздо чаще, чем другие. Например, общая статистика показывает, что самой популярной комбинацией является 1234, которая составляет около 11% всех возможных паролей. На втором месте находится комбинация 1111, составляющая 6%, а на третьем — 0000, с долей в 2%.
Если речь идет о паролях из 3 цифр, то известно, что таких паролей всего 60. Для этого нужно взять 10 цифр (от 0 до 9) и составлять из них 3-значные числа. Их будет ровно 60, например, 243, 541, 514, 132 и др.
Если у нас есть 3 цифры и мы должны составить пароль из них, то общее количество комбинаций составляет 1000. Это объясняется тем, что мы имеем 10 цифр для каждой позиции, т.е. 10*10*10=1000.
С другой стороны, пароли могут быть заданы не только цифрами, но и буквами или смешанными символами. Например, для пароля из 6 символов (буквы и цифры) можно из 36 возможных символов каждый раз выбрать один для каждой позиции, что дает нам 36^6 = 2.17×10^9 возможных комбинаций.
Кроме того, можно использовать двоичные коды для создания паролей. Так, 4-разрядный двоичный код позволяет получить 16 кодовых комбинаций, а пятиразрядный — 32, шестиразрядный — 64 и т.д. Количество комбинаций можно посчитать по формуле I^n, где n — количество позиций, а I — количество цифр/букв в каждой позиции.
Наконец, важно отметить, что пароли должны быть надежными, а значит, не следует использовать очевидные комбинации, такие как даты рождения, номера телефонов и т.д. Стандартные пароли типа «123456» и «qwerty» также очень уязвимы для взлома
Лучшим вариантом будет использовать длинные и сложные коды, состоящие из более 10 символов, включающих в себя буквы, цифры и специальные символы.
Сочетания с повторениями:
Сочетания с повторениями — это комбинации, где элементы могут повторяться. Они очень полезны в различных ситуациях, когда нам необходимо рассчитать количество комбинаций из некоторого набора элементов с повторениями.
В данном случае мы рассматриваем комбинации из 10 цифр. Задача состоит в том, чтобы определить, сколько разных комбинаций можно составить из этих 10 цифр, где каждая цифра может повторяться.
Для решения данной задачи мы можем использовать принцип сочетаний с повторениями. Принцип заключается в том, что для каждой позиции в комбинации мы имеем возможность выбрать любую из 10 цифр. Таким образом, общее количество комбинаций можно найти, умножив количество выборов для каждой позиции:
Количество комбинаций = количество выборов для первой позиции * количество выборов для второй позиции * … * количество выборов для последней позиции
В данном случае количество выборов для каждой позиции равно 10, так как мы можем выбирать любую из 10 цифр. Поскольку все позиции независимы друг от друга, мы можем умножить количество выборов для каждой позиции, чтобы найти общее количество комбинаций. Таким образом:
Общее количество комбинаций = 10 * 10 * 10 * 10 * 10 * 10 * 10 * 10 * 10 * 10 = 10^10 = 10 000 000 000
Таким образом, из 10 цифр мы можем составить 10 миллиардов различных комбинаций. Это очень большое число и демонстрирует мощь сочетаний с повторениями.
В заключение, сочетания с повторениями позволяют нам рассчитывать количество комбинаций из некоторого набора элементов с повторениями. В данном случае мы рассмотрели пример комбинаций из 10 цифр, где каждая цифра может повторяться. Общее количество комбинаций составляет 10 миллиардов.
Применение комбинаций в реальной жизни
Комбинаторика, или наука о комбинаторике, изучает различные комбинации и их свойства. В реальной жизни комбинаторика имеет широкое применение в различных областях, включая математику, статистику, информатику, экономику и другие.
Одно из наиболее распространенных применений комбинаторики — это расчет количества возможных комбинаций объектов или событий. Например, в задачах распределения билетов на мероприятие или вариантов меню для ресторана.
Комбинаторика также применяется в задачах планирования и оптимизации. Например, при планировании расписания занятий для учебного заведения, комбинаторика позволяет рассчитать все возможные комбинации групп предметов и учебных групп, учитывая ограничения ресурсов и времени.
Комбинаторика также используется в задачах комбинаторной оптимизации, когда необходимо найти наилучшую комбинацию из множества вариантов, удовлетворяющую определенным критериям. Например, в задачах передачи данных или сетевого планирования, комбинаторика позволяет найти оптимальное сочетание элементов сети, чтобы максимизировать скорость передачи данных или минимизировать стоимость строительства сети.
Комбинаторика также находит применение в задачах вероятности и статистики. Например, при расчете вероятности выпадения определенной комбинации в карточной игре или вероятности получения определенного результата в случайном эксперименте.
В итоге, комбинаторика является важным инструментом для решения различных задач в реальной жизни. Знание основных принципов комбинаторики позволяет анализировать и решать сложные проблемы, связанные с комбинаторными объектами и их комбинациями.
Применение комбинаций с повторением в реальной жизни
Одно из применений комбинаций с повторением можно найти в области статистики и вероятности. Если у нас есть набор из 5 цифр и мы хотим определить, сколько различных комбинаций мы можем получить, то применение комбинаций с повторением поможет нам найти ответ. Такая информация может быть полезна при анализе данных, создании прогнозов и принятии решений.
Также комбинации с повторением могут быть полезны при составлении паролей. Вариантов создания паролей с использованием определенного набора символов может быть огромное количество. Использование комбинаций с повторением позволяет обладателям систем исключения всех возможных комбинаций пароля, улучшая безопасность.
В сфере проектирования и архитектуры также можно найти применение комбинаций с повторением. Например, при планировании расположения объектов или элементов в пространстве, комбинации с повторением позволяют найти оптимальные варианты размещения. Кроме того, комбинации с повторением могут быть использованы при разработке дизайна и создании схем.
| Некоторые области применения комбинаций с повторением: |
| Статистика и вероятность |
| Создание паролей |
| Проектирование и архитектура |
Как вычислить число комбинаций
Количество сочетаний обозначается как C n m (читается: сочетания из \(n\) по \(m\)). Сочетания вычисляются по формуле C n m = n! M! ( n − m )!.
07.06.2023 Сколько всего возможно комбинаций из 3 цифр
Все мы хотя бы раз в жизни сталкивались с кодовыми замками, и часто нам приходилось задумываться о том, сколько же всего возможных комбинаций может быть у таких замков. На самом деле, это очень простой вопрос математики.
Для начала рассмотрим замок, который имеет три цифры в коде. Сколько же всего возможно комбинаций из трех цифр? Возможно, многие уже знают ответ, но давайте для полноты картины все же рассмотрим этот вопрос более подробно.
Для расчета количества комбинаций мы можем использовать формулу I^n, где n — количество позиций, а I — количество цифр, букв в одной позиции. В случае нашего кодового замка с тремя цифрами, мы имеем 10 возможных цифр (от 0 до 9) и три позиции, поэтому общее количество возможных комбинаций будет равно 10^3=1000. Это означает, что у нашего замка может быть 1000 разных комбинаций паролей.
Однако, стоит учесть, что при использовании замка для дверей, например, первая цифра может быть нулем, поэтому на самом деле число возможных паролей будет немного меньше — 999.
Кроме того, стоит упомянуть, что формула I^n работает не только для цифр, но и для других объектов, которые могут быть использованы в качестве комбинаций. Например, если у нас есть 5 букв (B, C, D, E, F), и мы хотим найти все возможные комбинации из 3 букв, то мы можем воспользоваться формулой Ckn=n!(n−k)!⋅k! И получим, что всего существует 10 комбинаций из трех букв, выбранных из пяти букв. Когда мы находим все комбинации из набора с 5 объектами, если мы берем 3 объекта за один раз, мы находим все 3-элементные подмножества.
Интересно также узнать, сколько всего возможных комбинаций можно составить из цифр 1, 2, 3 и 4. В данном случае, число возможных комбинаций будет равно 4^3=64. Если мы исключим комбинации, которые содержат только одну цифру (111, 222, 333 и т.д.), то останется 60 действительных комбинаций.
Что же касается вопроса о том, как рассчитать все возможные комбинации, то мы можем воспользоваться формулой Ckn=n!(n−k)!⋅k!, как уже упоминали выше. Например, если у нас есть 10 объектов, а мы хотим найти все возможные комбинации из 4 объектов, то C10^4=210, то есть всего существует 210 комбинаций из 10 объектов, выбранных по 4.
А что насчет максимального количества комбинаций? Здесь мы можем использовать формулу nCr = n! / р! (н-р)!, которая позволяет определить количество сочетаний из n объектов по k. Например, если у нас есть 6 объектов, а мы хотим найти все возможные сочетания по 3, то nCr=20. Это означает, что всего существует 20 различных сочетаний из 6 объектов, выбранных по 3.
Таким образом, мы рассмотрели несколько интересных вопросов, связанных с количеством возможных комбинаций. Понимание этой темы может быть полезным не только для тех, кто работает с кодовыми замками, но и для всех, кто интересуется математикой и логикой.






























