Извлечение корней
Представить работу калькулятора можно с помощью таблицы квадратов двузначных чисел. По горизонтали в каждом из столбцов указаны единицы от одного до девяти, по вертикали – десятки. Достаточно выяснить, в какой из ячеек находится подкоренное число. Несложно догадаться, что по горизонтали в левой крайней колонке указаны десятки, в верхней строчке таблицы – единицы.
Допустим, под корнем стоит 7056. Находим значение в таблице. Это 8 десятков и 4 единицы, число 84. То есть, 84 это квадратный корень онлайн из 7056. Онлайн-калькулятор находит значения любого подкоренного выражения по подобным таблицам.
При перемножении отрицательных величин получается величина, больше нуля. Извлечение арифметического квадратного корня возможно только из положительного числа (матрицы).
Вычисление квадратного корня
Ранее для выполнения арифметических операций мы использовали метод «столбика». А как производить вычисление квадратного корня? Существует несколько приемов, мы рассмотрим простейший из них.
Очевидно, что чем больше число, тем больше и его квадрат. Например, 5 > 4, поэтому и 52> 42. Значит, справедливо и обратное утверждение: чем больше число, тем больше и его квадратный корень.
![]()
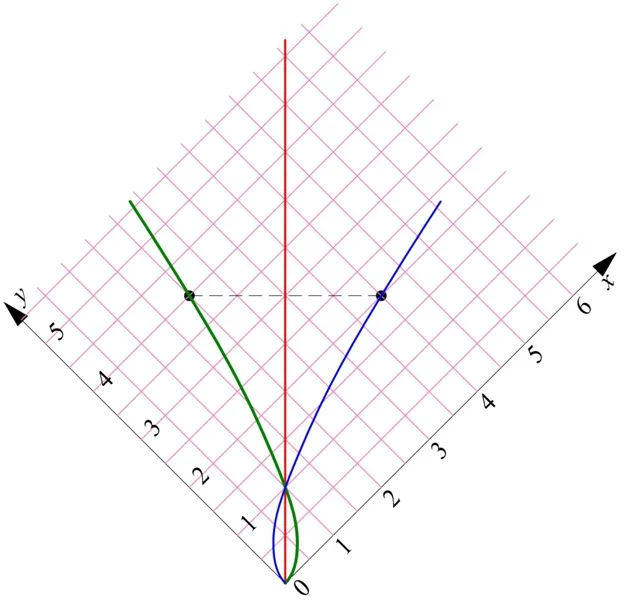
Убедиться в этом можно и с помощью графика функции у = х2. Будем отмечать на нем числа и их квадратные корни:
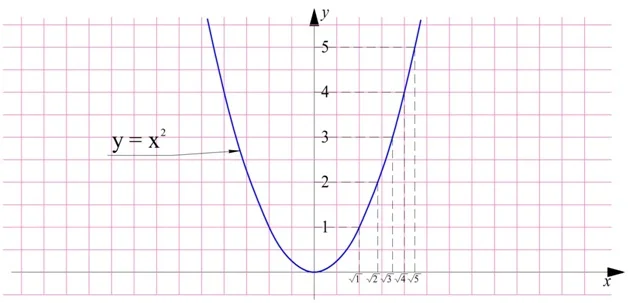
Видно, что чем выше на оси Оу располагается число, тем правее на оси Ох находится его квадратный корень.
Зная это свойство, легко оценить значение корня из любого числа. Продемонстрируем это на примере вычисления значение корня из 2. Нам известно, что
1 < 2 < 4
Значит, можно записать следующие неравенства:
Нам удалось определить, что корень из двух находится между единицей и двойкой, то есть
Теперь определим первую цифру после запятой для корня из двух. Будем возводить в квадрат десятичные дроби 1,1; 1,2; 1,3 и т. д, до тех пор пока не получим выражение, большее 2:
1,12 = 1,21
1,22 = 1,44
1,32 = 1,69
1,42 = 1,96
1,52 = 2,25
Теперь мы можем записать неравенства:
Получается, что корень имеет значение, находящееся между 1,4 и 1,5, то есть
Попытаемся определить ещё одну цифру после запятой:
1,412 = 1,999396
1,422 = 2,002225
Отсюда следует, что:
Продолжая подобные вычисления, можно вычислить любое количество знаков после запятой:
Конечно, на практике все вычисления выполняются компьютером, а не вручную. Однако программисты стремятся написать программы так, чтобы они работали как можно быстрее, то есть получали результат, выполняя меньшее количество вычислений. Поэтому на практике чаще используется метод бисекции (деления надвое), который отличается большей эффективностью. Для начала нужно найти очевидную оценку корня, например:
Получили, что корень из 2 находится между 1 и 2. Теперь найдем среднее арифметическое этих двух значений:
(1 + 2)/2 = 1,5
Возведем среднее арифметическое в квадрат:
1,52 = 2,25
Теперь мы можем записать неравенство
То есть искомое нами значение находится между 1 и 1,5. Снова найдем среднее этих двух оценок и возведем его в квадрат:
(1 + 1,5)/2 = 1,25
1,252 = 1,5625
Зная это, можем записать:
На каждом следующем шаге вычислений мы будем всё точнее определять оценки корня, при этом вычислений мы делаем не очень много.
Периодически могут встречаться задания, в которых надо грубо оценить значение квадратного корня.
Пример. Сколько целых чисел на координатной прямой располагается между
Решение: Ближайшие к числу 60 полные квадраты – это 64 и 49, поэтому можно записать:
Также можно оценить и корень из 140:
Получаем, что между корнями располагается четыре числа: 8, 9, 10 и 11:
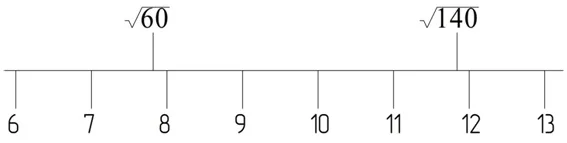
Ответ: 4
Метод Герона
Как поступить, когда необходимо хотя бы приблизительно знать, чему равен извлечённый корень (если невозможно получить целое значение)? Быстрый и довольно точный результат даёт применение метода Герона. Его суть заключается в использовании приближённой формулы:
√R = √a + (R — a) / 2√a,
где R — число, корень которого нужно вычислить, a — ближайшее число, значение корня которого известно.
Рассмотрим, как работает метод на практике, и оценим, насколько он точен. Рассчитаем, чему равен √111. Ближайшее к 111 число, корень которого известен — 121. Таким образом, R = 111, a = 121. Подставим значения в формулу:
√111 = √121 + (111 — 121) / 2 ∙ √121 = 11 — 10 / 22 ≈ 10,55.

Теперь проверим точность метода:
10,55² = 111,3025.
Погрешность метода составила приблизительно 0,3. Если точность метода нужно повысить, можно повторить описанные ранее действия:
√111 = √111,3025 + (111 — 111,3025) / 2 ∙ √111,3025 = 10,55 — 0,3025 / 21,1 ≈ 10,536.
Проверим точность расчёта:
10,536² = 111,0073.
После повторного применения формулы погрешность стала совсем незначительной.
Примеры вычисления корня.
Вычислить √6335289_______.
Будем записывать промежуточные результаты в столбик по аналогии с делением. Черновик справа от столбика.
6’33’52’89 | 2517.
−4____
233
−225 |45×5 ______
852
−501 |501×1 ________
35189
−35189 |5027×7__________
0
1) Разбиваем число на грани: 6’33’52’89. Получилось 4 штуки, следовательно, ответ будет состоять из 4-ёх цифр. Первая цифра 2, так как 22 = 4 2 = 9 > 6.
2) Далее удваиваем имеющуюся часть ответа, определяем остаток, сносим очередную грань и подбираем следующую цифру ответа. Повторяем этот шаг до последней грани:
233:40 ≈ 5; 45×5 = 225 233; следовательно, 2-я цифра 5;
852:500 ≈ 1; 501×1 = 501 852; следовательно, 3-я цифра 1.
3) Если целый корень существует, то его последней цифрой может быть либо 3, либо 7. Можем проверить 2513 и 2517 умножением в столбик. Но для многозначных чисел быстрее продолжить по общему алгоритму:
35189:5000 ≈ 7; 5027×7 = 35189 (!) Последняя цифра 7.
Ответ: 2517.
Вычислить √2304____.
48
×48
______
384
192
______
2304
Разбиваем на грани. 23’04. Следовательно, ответ из 2-ух цифр, первая цифра 4, т.к. 42 = 16 2 = 25 > 23. Последняя цифра либо 2, либо 8, т.к. результат умножения должен заканчиваться на 4.
Итак, 42 или 48? 42 ≈ 40; 402 = 1600. 48 ≈ 50; 502 = 2500. 2500 ближе к заданному числу, поэтому проверку умножением в столбик начинаем с 48.
Ответ: 48.
Это самый распространенный случай на ЕГЭ по математике, и я настоятельно рекомендую завершать его именно проверкой.
Вычислить √503___.
Число заканчивается тройкой. Сразу видно, что целого значения корня не получится. Зададимся вопросом, с какой точностью надо определить корень. Допустим, в условии сказано округлить ответ до сотых. Это означает, что получить его надо до тысячных, т.е. до 3-го знака после запятой. Поэтому к заданному числу нужно добавить еще 3 нулевые грани. И не забыть саму запятую!
5’03,00’00’00 | 22,427.
−4____
103
− 84 |42×2 ______
1900
−1776 |444×4 ________
12400
− 8964 |4482×2 __________
343600
−313929 |44847×7 ____________
29671
1) Таким образом, разбиение на грани будет таким 5’03,00’00’00. Ответ будет состоять из пяти цифр — 2 до запятой и 3 после. Первая цифра равна 2 (22 = 4 2 = 9 > 5), последнюю цифру в данном случае мы определить не можем.
2) Далее, выполняем шаги 4,5,6 общего алгоритма, как обычно:
103:40 ≈ 2; 42×2 = 84 103; следовательно, 2-я цифра 2.
1900:440 ≈ 4; 444×4 = 1776 1900; следовательно, 3-я цифра 4.
12400:4480 ≈ 3; 4483×3 = 13449 > 12400; 4482×2 = 8964
343600:44840 ≈ 8; 44848×8 = 358784 > 343600; 44847×7 = 313929
Мы еще не получили нулевого остатка и, может быть, не получим никогда, если искомый корень иррациональное число. Но нам это и не нужно, т.к. результат уже получен с нужной для округления точностью.
По отбрасываем 3-ю цифру после запятой, увеличив (т.к. 7 > 5) предыдущую на единицу 22,427 ≈ 22,43.
Ответ: 22,43.
Вычислить √1,5____.
Чтобы вычислить корень из десятичной дроби, нужно вспомнить, что 102 = 100 и 0,12 = 0,01. Т.е. при возведении в квадрат происходит удвоение разрядов. Соответственно, для извлечении квадратного корня из десятичной дроби нам нужно, чтобы она имела четное число цифр после запятой. В этом случае мы получим целое число граней после запятой при разбиении справа налево (с конца), а значит и целое число цифр в дробной части ответа.
Вспомним также, что к целой части числа можно дописывать сколько угодно нулей впереди, а к дробной — сколько угодно нулей в конце. Число от этого не меняется.
I способ.
√1,5___√1,50____
Допустим, что нужно дать ответ с точностью до десятых, тогда вычислять значение этого корня нужно до второго знака после запятой. Сейчас у нас 2 цифры после запятой, т.е. одна грань, поэтому добавим еще одну нулевую грань.
1,50’00 | 1,22
−1____
50
−44 |22×2______
600
−484 |242×2_______
116
1) Рабиение на грани: 1,50’00. Результат будет из 3-ёх цифр — одна до запятой и две после. Первая цифра, очевидно, 1.
2) Далее действуем по алгоритму:
50:20 ≈ 2; 22×2 = 44 50; следовательно, 2-я цифра 2.
600:240 ≈2; 242×2 = 484 600; следовательно, 3-я цифра 2.
3) Округляем 1,22 ≈ 1,2.
Ответ: 1,2.
II способ.
Умножаем и одновременно делим наше число на 10 в четной степени ( обязательно в четной, чтобы потом легко и точно извлечь корень из знаменателя). 1,5 = 1,5 × 100/100 = 150/100. Следовательно, нужно вычислить корень из 150 и разделить его на корень из 100, т.е. на 10.
здесь√150____√1,5____
Ответ: 1,2.
Внимание: очень распространена ошибка, когда для определения примерного значения корня из 1,5 берут корень из 15. Запомним — четное количество нулей.√10__ ≈ 3,16 √100___ = 10 √1000____ ≈ 31,62 √10000_____ = 100 √100000______ ≈ 316,23 √1000000_______ = 1000
Проблемы при работе с комплексными числами
- Отсутствие физической интерпретации: Действительные числа можно интерпретировать как позиции на числовой прямой, а комплексные числа не имеют такой возможности. Это может затруднить понимание смысла операций над комплексными числами.
- Сложность умножения и деления: При умножении или делении комплексных чисел требуется умножение двух сумм и вычисление двух произведений. Это может быть времязатратно и трудно для понимания.
- Несимметричность: У комплексных чисел нет коммутативности, их умножение не является коммутативным. Это означает, что a + bi * c + di ≠ c + di * a + bi. Это может быть причиной ошибок при работе с комплексными числами.
- Сложность визуализации: Комплексные числа можно представить в виде точек на плоскости, где действительная ось — это ось x, а мнимая ось — это ось y. Однако, визуализация сложных операций, таких как возведение в степень, может быть сложной и неинтуитивной.
- Нерациональность: Большинство комплексных чисел являются нерациональными и не могут быть представлены в виде десятичной или обыкновенной дроби. Это может затруднить их использование в реальных задачах.
Несмотря на эти проблемы, комплексные числа широко применяются в различных областях науки, техники и математики, включая электротехнику, теорию вероятностей и физику.
Математические основы
Корень — это операция в математике, которая позволяет найти число, при возведении которого в указанную степень получается данное число. В случае корня из 25, мы ищем число, при возведении во вторую степень, даёт 25. Таким числом является 5, так как 5^2 = 25.
Корни являются важной частью математики и широко используются в различных дисциплинах. Они позволяют решать уравнения, находить значения функций, а также анализировать графики
Понимание основных математических понятий и операций, таких как корень, является важным для успешного решения математических задач и общего развития.
Другие примеры вычисления корня квадратного
Корень квадратный — это арифметическая операция, которая позволяет найти число, при возведении в квадрат которого получается заданное число. Нахождение квадратного корня является одной из задач математической алгебры.
Другим примером вычисления корня квадратного является нахождение корня кубического. Кубический корень из числа x — это такое число y, что при возведении его в куб равно x. Кубический корень можно записать в виде ∛x.
Если мы хотим найти корень n-степени из числа, мы можем воспользоваться таким алгоритмом:
1. Задаем число, из которого нужно найти корень, и n-степень.
2. Приближаемся к искомому значению с помощью итераций.
3. Пересчитываем значение корня с использованием найденного приближения.
4. Повторяем шаги 2 и 3, пока не получим достаточно точное значение.
Метод нахождения корня квадратного также известен как метод золотого сечения. Для нахождения корня квадратного из числа можно использовать специальные алгоритмы или калькуляторы, которые позволяют производить такие вычисления.
Корень квадратный из числа, который не является квадратом рационального числа, называется иррациональным числом. Он не может быть точно выражен в виде десятичной дроби или квадратного корня.
Если вам интересно узнать больше о корнях квадратных и других математических понятиях, вы можете обратиться к специальным математическим книгам, словарям или искать полезное содержание в Интернете. Также существуют видео и ссылки, которые подробно объясняют свойства корня квадратного и его значение в алгебре.
Если у вас возникли вопросы или вы хотите поделиться своими примерами вычисления корня квадратного, см в примечаниях!
Как извлечь квадратный корень из числа?
Чтобы извлечь квадратный корень из числа, надо задать себе вопрос: какое число в квадрате даст выражение под корнем?
Например. Извлеките корень: а)\(\sqrt{2500}\); б) \(\sqrt{\frac{4}{9}}\); в) \(\sqrt{0,001}\); г) \(\sqrt{1\frac{13}{36}}\)
а) Какое число в квадрате даст \(2500\)?
\(\sqrt{2500}=50\)
б) Какое число в квадрате даст \(\frac{4}{9}\)?
\(\sqrt{\frac{4}{9}}\)\(=\)\(\frac{2}{3}\)
в) Какое число в квадрате, даст \(0,0001\)?
\(\sqrt{0,0001}=0,01\)
г) Какое число в квадрате даст \(\sqrt{1\frac{13}{36}}\)? Чтобы дать ответ на вопрос, нужно перевести смешанную дробь в неправильную.
\(\sqrt{1\frac{13}{36}}=\sqrt{\frac{49}{16}}=\frac{7}{6}\)
Замечание: Хотя \(-50\), \(-\frac{2}{3}\), \(-0,01\),\(- \frac{7}{6}\), тоже отвечают на поставленные вопросы, но их не учитывают, так как квадратный корень – всегда положителен.
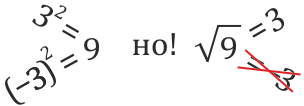
Что такое корень числа?
Корень n-й степени из числа x — это такое число r, которое в степени n равняется x. Или другими словами: rn= x.
Эта запись с математическим корнем из числа х в n-ой степени имеет собственное название в каждом символе:
- n — здесь является степенью или показателем корня, n всегда является натуральным числом, таким, как — 1, 2, 3 и так далее.
- х — здесь является выражением или подкоренным числом. Выражается, как вещественное или любое комплексное число.
- √ — здесь является символом корня или знаком, имеющим еще другое название — радикал.
Например:
Такое выражение читается, как корень третьей степени от числа 8. Это корень равняется двум. Число 3 здесь является степенью корня, а число 8 – подкоренным числом.
В математике нахождение корня называется «извлечение корня».
Причём важно разделять понятия арифметического и алгебраического корня
Арифметический или алгебраический (общий)
Арифметический корень n-й степени из неотрицательного вещественного числа a — это неотрицательное число b, для которого bn=a. Обозначается арифметический корень знаком радикала (про который мы уже сказали выше).
Арифметический корень второй степени из числа a (√a) — это неотрицательное число b (b ≥ 0), при котором выполняется равенство b2 = a. К примеру, корнями второй степени из числа 16 являются корни 4 и −4, но арифметическим из них является только корень 4.
Таким образом, арифметический корень, в отличие от корня общего вида (или алгебраического), определяется только для неотрицательных вещественных чисел, а его значение всегда существует, однозначно и неотрицательно.
Далее мы будем говорить именно про арифметические корни.
Наиболее часто используемые корни — это корни второй степени и корни третьей степени. Они даже имеют собственные названия:
- Квадратный корень
- Кубический корень
Квадратный корень
Квадратный корень – это корень со степенью два. Чаще всего, в значении радикала степень «два» не прописывается, а просто используется символ √.
Арифметический квадратный корень всегда является положительным числом, и кроме того подкоренное значение также всегда положительно.
Почему все происходит именно так, нам расскажет простой пример с решением:
- Ищем квадратный корень из -16.
- Логично предположить в ответе — 4.
- Но если проверить таким образом: 4*4 = 16 — то нет, не сходится.
- Если — 4, то -4 * -4 = 16, нужно отметить, что минус на минус всегда в итоге дает плюс.
Ни одно число при возведении его в квадрат не дает отрицательного результата.
Вывод: все числа, которые стоят под знаком корня, всегда должны быть положительными.
Кубический корень
Кубический корень – это такое число, которое для получения подроренного числа нужно умножить само на себя три раза.
К примеру, кубический корень из 64 будет равен «4».
Решение будет выглядеть так: 4х4х4 = 64.
Преобразование выражений с квадратными корнями
Изученные правила помогают преобразовывать некоторые выражения. Так, можно вынести множитель из-под знака корня:
Это действие может использоваться для сложения корней, у которых, казалось бы, стоят разные числа под знаком радикала:
![]()
Обратное действие называют внесением множителя под знак корня:
![]()
Пример. Какое число больше
Решение. Внесем множитель под знак корня:
Из двух корней больше тот, у которого больше подкоренное выражение, поэтому
Из этого следует, что
Заметим, что под знак радикала может быть внесен исключительно неотрицательный множитель! Знак минуса должен остаться перед радикалом:
Принято считать, что с дробью, содержащей радикал, проще работать, когда этот радикал находится в числителе, а не знаменателе. В связи с этим стремятся избавиться от иррациональности в знаменателе. В простейшем случае дробь просто домножают на квадратный корень:
Как видим, корень «переехал» из знаменателя в числитель. Несколько сложнее производится освобождение от иррациональности, если в знаменателе стоит сумма или разность корней. В этом случае помогает формула :
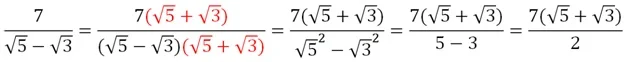
Рассмотрим несколько задач.
Пример. Найдите наибольшее значение выражения
Решение. По формуле разности квадратов можно записать:
Зная это, заменим знаменатель дроби:
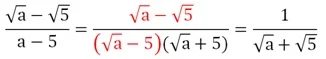
Эта дробь принимает наибольшее значение тогда, когда ее числитель, наоборот, принимает минимальное значение. Это произойдет при а = 0, так как арифметический квадратный корень не может быть отрицательным. Тогда наибольшее значение дроби будет составлять
Пример. Упростите выражение
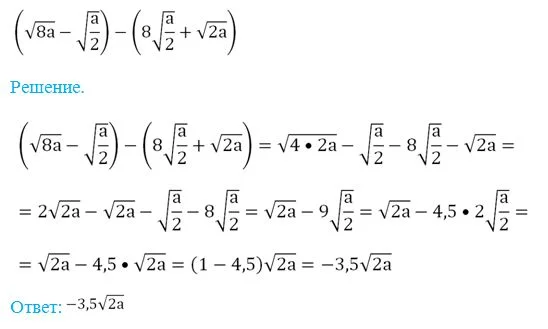
Довольно тяжелым является случай, когда под знаком корня находится другой корень. Выражения вида
называют двойным радикалом.
Существует формула двойного радикала, с помощью которой его можно иногда упростить:
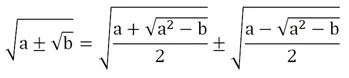
Для доказательства справедливости этого тождества возведем его правую часть в квадрат, используя (х ± у)2 = х2 ± 2ху + у2:
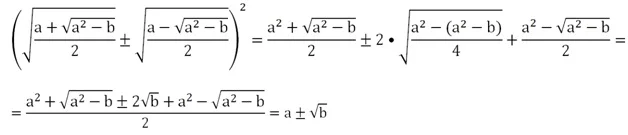
Принципиально важно, что величина а2 – b должна быть неотрицательной. Рассмотрим преобразование двойных радикалов на примере
Пусть надо освободиться от внешнего радикала в выражении
Для этого сначала внесем двойку под знак внутреннего радикала, а потом воспользуемся формулой:
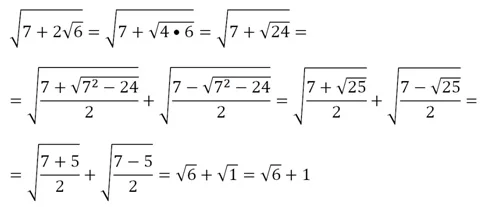
Заметим, что формула двойного радикала полезна в том случае, если выражение а2 – b является полным квадратом.
Как посчитать корень из 25?
Корень из 25 можно посчитать с помощью операции извлечения квадратного корня. Корень из числа выражает значение, которое нужно возвести в квадрат, чтобы получить исходное число.
Чтобы посчитать корень из 25, мы можем использовать различные методы:
- Использование функции или оператора для вычисления квадратного корня, доступного в большинстве языков программирования.
- Применение математической формулы, в которой корень из 25 представлен как число возводимое в степень 0.5: √25 = 250.5 = 5.
- Использование калькулятора, на котором есть функция вычисления квадратного корня.
Вот примеры использования этих методов:
- В Python:
В Java:
В JavaScript:
Используя математическую формулу:
В результате выполнения любого из этих методов мы получим ответ — корень из 25 равен 5.
История открытия
История открытия корня из 25 имеет свои корни в античных временах. Уже древнегреческие математики знали о существовании числа, квадрат которого равен 25. Они называли его пентагон, так как он имел пять сторон.
Однако, долгое время число 5 и его корень оставались загадкой для ученых. Различные культуры и цивилизации создали свои версии и объяснения этому феномену.
И только благодаря развитию математики и ее прикладных наук, в XIX веке было доказано, что корень из 25 равен пяти. Математики использовали специальные методы и алгоритмы для нахождения корней из чисел. Таким образом, получилось установить точное значение корня из 25.
Современные ученые используют корень из 25 в своих исследованиях и приложениях, например, в геометрии, статистике, физике или экономике. Он является одним из фундаментальных понятий в математике и имеет множество практических применений.
Корень квадратный из 16: объяснение и доказательство
Корень квадратный из числа представляет собой число, при возведении в квадрат которого получается данное число. В алгебре это полезное понятие позволяет найти значение корня и решать математические задачи.
Определение корня квадратного можно записать следующим образом:
Если x^2 = a, то x — корень квадратный из числа a.
Корень квадратный из 16 можно найти различными способами. Один из них — использование арифметического метода. Поделитесь своим калькулятором или используйте метод итераций, чтобы найти корень квадратный из 16: числа, которое, при возведении в квадрат, будет равно 16.
Если вы не хотите использовать калькулятор и не знаете такого алгоритма, как метод итераций, можно воспользоваться другим приемом. Корень квадратный из 16 равен 4, так как 4 * 4 = 16.
Корень квадратный от числа может быть как целым числом, так и иррациональным числом. В случае с корнем квадратным из 16, он является целым числом.
Значение корня квадратного может быть выражено в виде иррационального числа, как, например, корень из 2 или корень из 3. Эти числа являются корнями квадратными, так как их квадраты равны 2 и 3 соответственно.
Корень квадратный из 16 равен 4, так как 4 * 4 = 16. Это пример квадратного корня, который является целым числом.
Исторически первые записи о квадратных корнях появились в Вавилонском математическом трактате «Золотое тождество». В трудах математика Рамануджана и других ученых можно найти многочисленные свойства и интересные факты о квадратных корнях.
Видео и ссылки на дополнительные материалы по теме:
1. Корень квадратный из 16: объяснение и применение в практике
Сколько корней квадратных у числа 25?
Число 25 имеет два корня квадратных: положительный и отрицательный. Корень квадратный из 25 равен 5, а корень квадратный из -25 равен -5. В обоих случаях, возведя корень в квадрат, мы получим исходное число 25.
2. Квадратный корень и его свойства
Заключение:
Как доказать, что корень квадратный из 25 равен 5?
Для доказательства того, что корень квадратный из 25 равен 5, нужно возвести 5 в квадрат и проверить, получится ли 25. В данном случае, 5 * 5 = 25, что означает, что корень квадратный из 25 равен 5. Это можно проверить, просто вычислив квадрат 5 и убедившись, что получим 25.
Корень квадратный из 16 равен 4. Это числом, при возведении в квадрат которого получается 16. Корень квадратный может быть как целым числом, так и иррациональным числом. Применение корня квадратного широко распространено в математике и позволяет решать различные задачи.
Вопросы для самопроверки:
1. Какой корень квадратный из числа 16?
2. Чему равен квадратный корень из 16?
3. Является ли 4 корнем квадратным числа 16?
4. Как можно найти корень квадратный из числа, не используя калькулятор?
Примечания:
— В данной статье рассмотрен квадратный корень, но также существует кубический корень и корни n-ой степени.
— Квадратный корень из арифметическими свойствами имеет множество математических тождеств, которые могут быть использованы в практике.
— Для более глубокого изучения темы рекомендуется обратиться к специальной литературе и ресурсам по алгебре.
Чему равен корень квадратный из 25 и почему 5 -5 или только 5Корень квадратный из 25
Contents
Исследование значения корня

Здравствуйте! Сегодня мы с вами поговорим о значении корня квадратного и ответим на вопрос: почему корень из 25 равен не только +5, но и -5?
Давайте начнем с основ. Что такое корень квадратный? Корень квадратный числа — это такое число, которое при возведении в квадрат дает исходное число. Например, корнем квадратным числа 25 является число 5, потому что 5 в квадрате равно 25. Но на этом история не заканчивается.
Когда мы говорим о корне квадратном, мы имеем в виду два числа: положительное и отрицательное. Это связано с тем, что при возведении числа в квадрат оно может быть и положительным, и отрицательным. Таким образом, корень квадратный из 25 имеет два значения: +5 и -5. При подставлении этих значений в формулу, получаем следующее выражение: (+5)^2 = 25 и (-5)^2 = 25. Оба выражения верны.
Теперь давайте разберемся, почему корень квадратный из 25 может быть и +5, и -5. Представьте, что у вас есть загадка, и вы знаете, что ответ на нее 25. Всего лишь зная этот факт, вы можете предположить, что ответ может быть и 5, и -5, так как при возведении этих чисел в квадрат мы получим искомое значение. Это подобно ситуации, когда вы решаете уравнение в той или иной степени и ищете все возможные решения.
Важно понимать, что значения корня квадратного могут быть разными в разных контекстах. Например, если мы говорим о физических величинах, то большинство из них имеют только положительные значения
Таким образом, корень квадратный из 25 в контексте физических величин будет равен только +5. Но если мы рассматриваем математические задачи, то корень из 25 будет иметь два значения: +5 и -5.
Итак, если кто-то говорит, что корень квадратный из 25 равен только +5 или только -5, то это не полностью соответствует действительности. правда состоит в том, что корень квадратным из 25 равен и +5, и -5. Это результат возведения в квадрат исходного числа, и оба значения верны.
Надеюсь, теперь вы понимаете, почему корень квадратный из 25 равен и +5, и -5. Корень квадратный — удивительное математическое понятие, которое помогает нам находить решения уравнений, находить длины сторон прямоугольных треугольников и анализировать данные
Это один из фундаментальных элементов в математике, и его понимание поможет вам лучше разбираться в различных задачах и ситуациях, где важно знать значения корня квадратного
Функция квадратного корня
Каждому числу соответствует не более чем 1 арифметический квадратный корень. Поэтому формула
задает функцию. Исследуем ее.
Так как под знаком радикала может находиться лишь неотрицательное число, то областью определения корня является множество всех неотрицательных чисел. Такова же и область допустимых значений.
Построим график квадратного корня по точкам. Для этого вычислим ее значения в нескольких точках (указана точность до 0,1):

График функции квадратного корня будет выглядеть так:
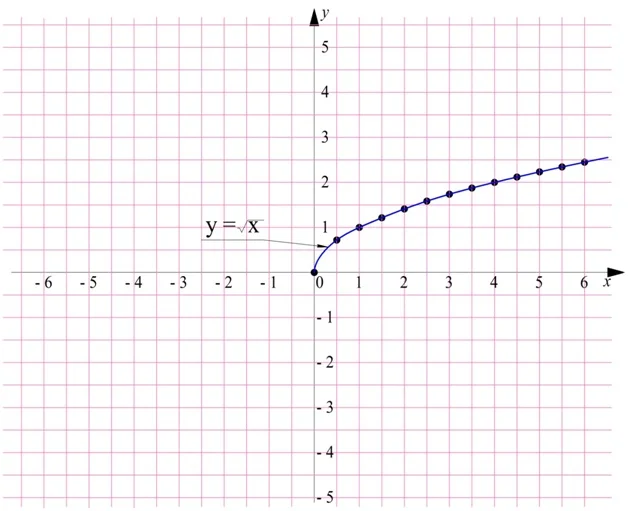
Отметим, что полученная линия чем-то напоминает обычную параболу функции у = х2, которую «положили набок», то есть повернули против часовой стрелки на 90°, а после убрали одну из ветвей:
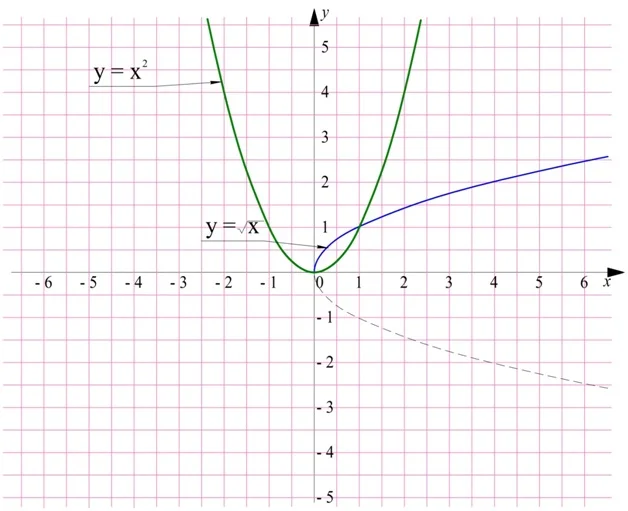
И это не случайность. Дело в том, что две эти функции являются обратными друг другу. Действительно, пусть с помощью графика параболы мы хотим найти значение величины а2. Стрелки показывают последовательность действий:
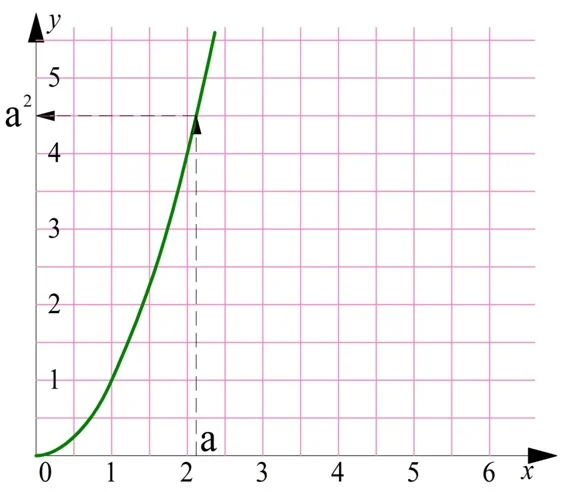
Мы должны найти а на оси Ох, построить от найденной точки вертикальную линию до пересечения с графиком, а потом провести горизонтальную линию. Но если нам надо вычислить корень из положительного числа b, то мы должны действовать в обратном порядке: найти b на вертикальной оси, провести горизонтальную линию до пересечения с параболой, и потом опустить перпендикуляр на горизонтальную ось:
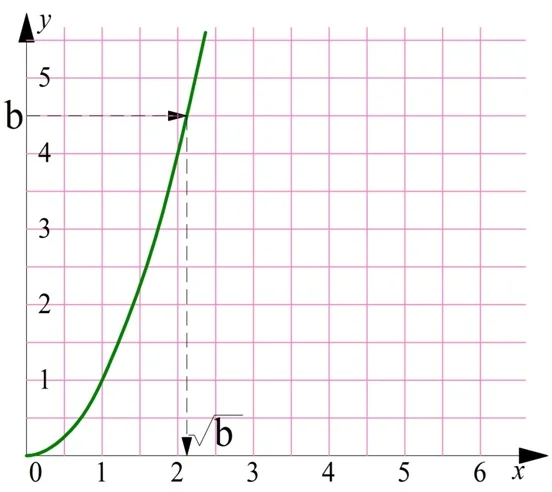
Получается, для вычисления обеих функций можно использовать один график! Но, так как традиционно аргумент функции обозначают буквой х, а саму функцию как у, а также ось Ох располагают горизонтально, то для получения графика обратной функции надо буквально повернуть график основной функции так, чтобы оси Ох и Оу поменялись местами:
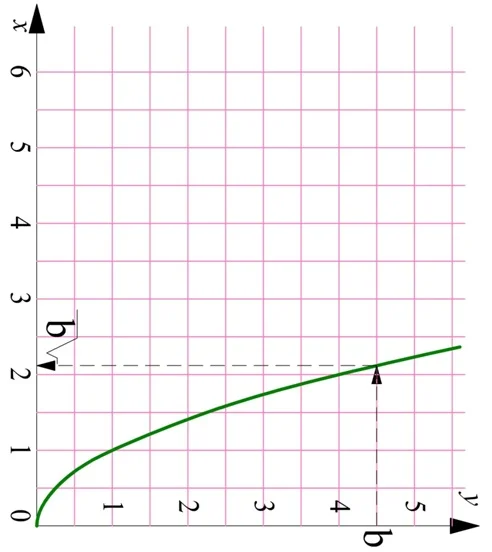
Действительно, в результате поворота получили уже знакомый график функции корня из х. Осталось лишь правильно переименовать оси и повернуть цифры в привычное положение.
Взаимное расположение этих графиков можно описать и иначе. Они симметричны относительно прямой линии, которую задает график у = х. Ведь если точка имеет координаты (а; b) принадлежит параболе у = х2, то, по определению корня, точка с обратными координатами (b; а) должна лежать на графике корня. Однако две такие точки будут симметричны относительно линии у = х:
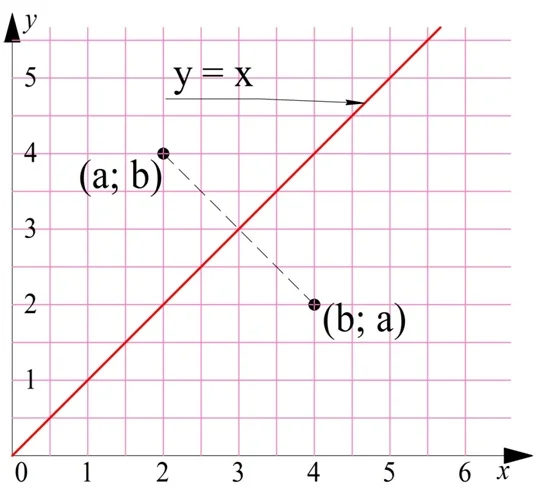
Соответственно, симметричны относительно этой прямой и графики обратных функций:
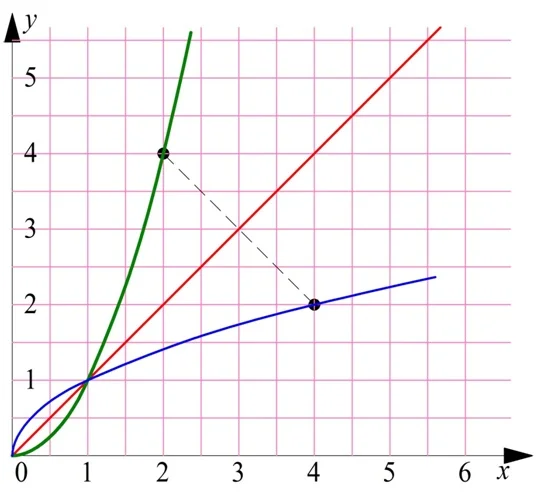
Исключительно для большей наглядности (чтобы была очевидна симметрия, о которой идет речь), повернем эту картинку на 45°:
Анализ алгоритма вычисления корня и его ошибки
Стандартный алгоритм вычисления корня из числа основывается на итерационном подходе. В начале выбирается начальное приближение для корня, а затем выполняются итерации до достижения необходимой точности. Ошибка в вычислении корня может возникнуть из-за нескольких факторов:
- Начальное приближение: Выбор неоптимального начального приближения может привести к большой ошибке в результате вычисления. Например, если начальное приближение выбрано слишком далеко от искомого корня, то количество итераций для достижения нужной точности может быть слишком большим.
- Округление и точность: Во время итераций, значения могут округляться до определенного количества знаков после запятой. Это может привести к накоплению ошибок и недостаточной точности вычисления. Например, если округление происходит до двух знаков после запятой, то результатом вычисления корня из 25 может стать значение, отличное от 5.
- Алгоритмические ограничения: Многие алгоритмы вычисления корня использовать приближения и упрощения, которые могут привести к ошибкам. Например, алгоритм может включать в себя предварительное определение диапазона возможных значений и выбор подходящего метода вычисления в зависимости от исходных данных. Однако, такие ограничения могут привести к получению неверного результата в некоторых случаях.
В результате, вычисление корня может привести к некорректному результату, отличному от ожидаемого значения. Для уменьшения ошибок в вычислении корня необходимо тщательно выбирать начальные приближения, учитывать округление и точность вычислений, а также анализировать ограничения и особенности используемых алгоритмов.
Заключение
Оказывается, что корень квадратный может использоваться не только для решения математических задач, но и в повседневной жизни. Например, если вам нужно посчитать расстояние от одной точки до другой по прямой линии, то для этого можно воспользоваться формулой нахождения расстояния между двумя точками в декартовой системе координат. В этой формуле вычисление расстояния осуществляется с помощью корня квадратного.
В математике корень квадратный также широко применяется при решении уравнений, нахождении площади прямоугольника и других геометрических фигур, а также при нахождении значений функций.
Таким образом, корень квадратный – это важная и полезная математическая операция, которая находит применение и в математике, и в реальной жизни. Понимание и умение использовать корень квадратный позволяет нам решать различные задачи и облегчает наше ежедневное существование.




























