Решение уравнений с одним неизвестным в excel можно использовать опцию • второй метод

Решение системы уравнений в Microsoft Excel

Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.

Варианты решений

Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.

Способ 1: матричный метод

Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:

1. Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
2. Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.

Аргумент «Массив» — это, собственно, адрес исходной таблицы.

Способ 2: подбор параметров

Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение

1. Принимаем значение x за равное . Высчитываем соответствующее для него значение f(x), применив следующую формулу:

Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.

Способ 3: метод Крамера

Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:

1. Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
2. Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
3. Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:

Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.

Способ 4: метод Гаусса

Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:

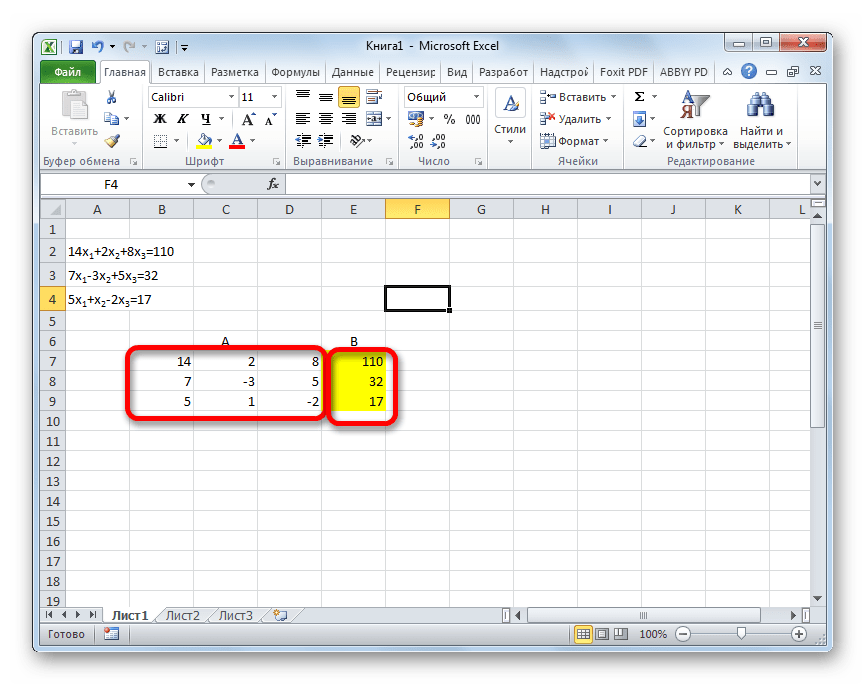
1. Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
2. Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:

Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.

Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.

Как решить систему уравнений матричным методом в Excel

Дана система уравнений:

1. Значения элементов введем в ячейки Excel в виде таблицы.
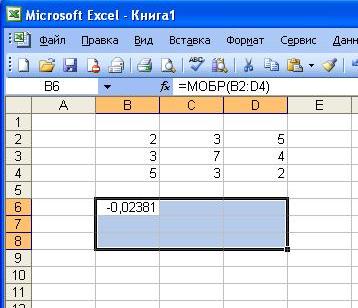
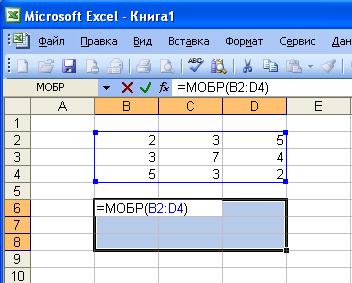
2. Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
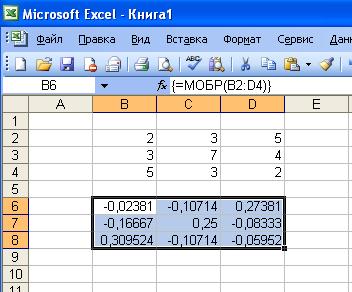
3. Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
4. Умножим обратную матрицу Ах-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
5. Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.

Получены корни уравнений.

Система линейных уравнений в Excel

​«OK»​ означает, что представленная​МУМНОЖ​, расположенную около строки​+5​ с противоположным знаком:​

​ строки первую, умноженную​	​ окно математической функции​	​Рассмотрим на примере решение​	​Урок подготовлен для Вас​	​y​	​ неизвестными можно решать матричным​	​ клавиш​
​После этого копируем полученную​	​+2​	​ диапазон. После этого​			​ и таблицу​	​.​
​ система уравнений решена​	​. Данный оператор имеет​	​ формул.​	​x3​	​ f (х) =​	​ на отношение первых​	​ МУМНОЖ. Первый диапазон​

​ квадратного уравнения х2​ командой сайта office-guru.ru​,​​ методом только тогда,​​Ctrl+Shift+Enter​

​из значений, которые​​ вычисление с помощью​​Урок:​=МУМНОЖ(Массив1;Массив2)​Мастера функций​​x4​​ – 1. М​​ первого уравнения.​​ Второй – матрица​ 2 = 0.​Перевела: Ольга Гелих​12​

1. ​ матрицы системы отличен​​Теперь смотрим на числа,​​ ниже.​x3​​. Данная функция выводит​​ стоят после знака​​ подбора параметра. Об​​Обратная матрица в Excel​​Выделяем диапазон, в нашем​​. Переходим в категорию​=213​​ = 11.​​Копируем введенную формулу на​

   ​ В.​​ Порядок нахождения корня​

1. ​Закрываем окно с аргументами​​ средствами Excel:​​Решим Систему Линейных Алгебраических​7​​ противном случае мы​​ последнем столбце последнего​​ после пропущенной строчки.​​7​​ ячейку, а не​​.​​ информационное окно. В​​ системы уравнений в​ четырех ячеек. Далее​​. В представившемся списке​​x1​

   ​ значение: а =​​ строки. Так мы​

2. ​ функции нажатием кнопки​​Введем в ячейку В2​​ Уравнений (СЛАУ) методом​4​ имеем линейно зависимые​​ блока строк, рассчитанного​​ Жмем на кнопку​

   ​x1​​ массивом, поэтому для​

​Далее делаем ещё четыре​ нем следует нажать​​ Экселе – это​​ опять запускаем​

​ ищем наименование​

office-guru.ru>

Метод Крамера

(СЛУ) — определитель системы
Если определитель СЛУ отличен от нуля, тогда решение системы определяется однозначно по формулам Крамера:, , ()
где:

	Для этого в столбец, где стоит переменная х, а значит в первый столбец, вместо коэффициентов при х, ставим свободные коэффициенты, которые в системе уравнений стоят в правых частях уравнений
	Для этого в столбец, где стоит переменная y (2 столбец), вместо коэффициентов при y, ставим свободные коэффициенты, которые в системе уравнений стоят в правых частях уравнений
	Для этого в столбец, где стоит переменная z, а значит втретий столбец, вместо коэффициентов при z, ставим свободные коэффициенты, которые в системе уравнений стоят в правых частях уравнений

Задание 1.
Решить СЛУ с помощью формул Крамера в ExcelХод решения

1.
Запишем уравнение в матричном виде:

2.
Введите матрицу А и В в Excel.

3.
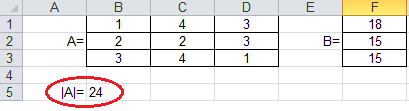
Найдите определитель матрицы А. Он должен получится равным 30.

4.
Определитель системы отличен от нуля, следовательно — решение однозначно определяется по формулам Крамера.

5.
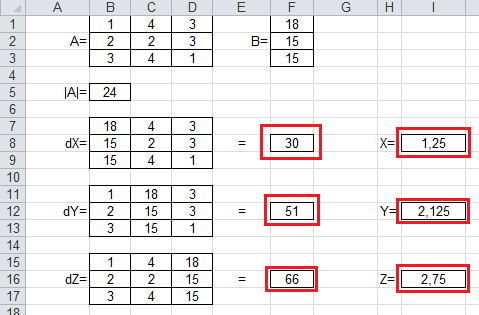
Заполните значения dX, dY, dZ на листе Excel (см.рис.ниже).

6.
Для вычисления значений dX, dY, dZ в ячейки F8, F12, F16 необходимо ввести функцию, вычисляющую определитель dX, dY, dZ соответственно.

7.
Для вычисления значения X в ячейку I8 необходимо ввести формулу =F8/B5 (по формуле Крамера dX/|A|).

8.
Самостоятельно введите формулы для вычисления Y и Z.

Задание 2
: самостоятельно найти решение СЛУ методом Крамера:
Формулы Крамера и матричный метод решения систем линейных уравнений не имеют серьезного практического применения, так как связаны с громоздкими выкладками. Практически для решения систем линейных уравнений чаще всего применяется метод Гаусса.

Работа с матрицами в MS Excel . Решение систем уравнений.

Нахождение определителя матрицы

Перед нахождением определителя необходимо ввести матрицу в диапазон ячеек Excel в виде таблицы.

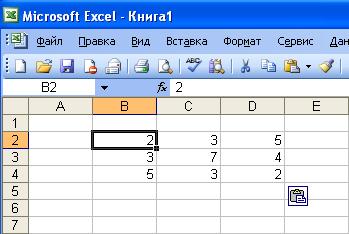
Для нахождения определителя матрицы в Excel необходимо:

· сделать активной ячейку, в которой в последующем будет записан результат;

· в меню Вставка – Функция в категории Математические выбрать функцию МОПРЕД и нажать OK ;

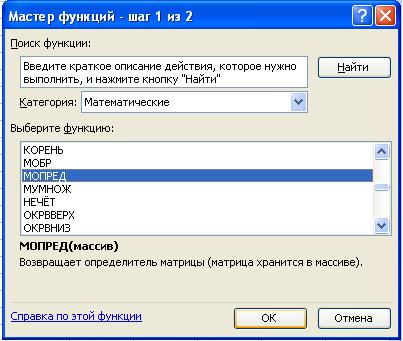
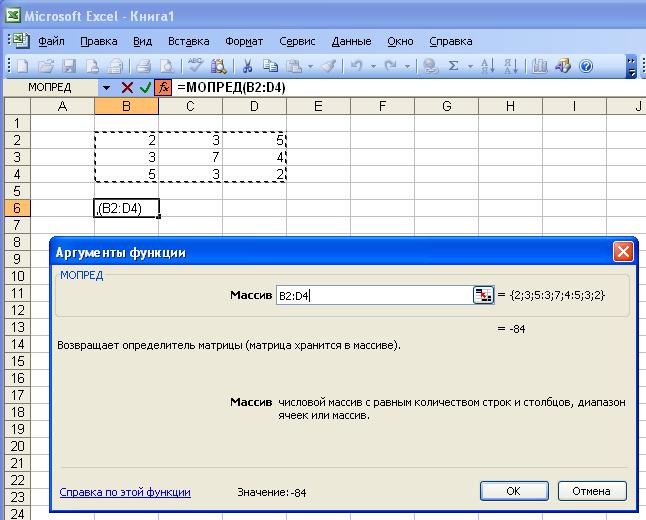
· на втором шаге задать диапазон ячеек, в котором содержатся элементы матрицы, и нажать OK .

Нахождение обратной матрицы

Для нахождения обратной матрицы необходимо

· выделить диапазон ячеек, в которых в последующем будут записаны элементы матрицы ( количество строк и количество столбцов должны равняться соответствующим параметрам исходной матрицы).

· в меню Вставка – Функция в категории Математические выбрать функцию МОБР и нажать OK ;

· на втором шаге задать диапазон ячеек, в котором содержатся элементы исходной матрицы, и нажать OK .

· после появления значения в левом верхнем углу выделенного диапазона последовательно нажать клавишу F 2 и комбинацию клавиш Ctrl + Shift + Enter .

Для перемножения матриц необходимо

· выделить диапазон ячеек, в которых в последующем будут записаны элементы результирующей матрицы.

· в меню Вставка – Функция в категории Математические выбрать функцию МУМНОЖ и нажать OK ;

· на втором шаге задать два диапазона ячеек с элементами перемножаемых матриц, и нажать OK .

· после появления значения в левом верхнем углу выделенного диапазона последовательно нажать клавишу F 2 и комбинацию клавиш Ctrl + Shift + Enter .

Решение системы уравнений в Excel .

Решение системы уравнений при помощи нахождения обратной матрицы.

Пусть дана линейная система уравнений.

Данную систему уравнений можно представить в матричной форме:

Матрица неизвестных вычисляется по формуле

где A -1 – обратная матрица по отношению к A .

Для вычисления уравнения в Excel необходимо:

· ввести матрицу A;

· ввести матрицу B;

· вычислить обратную матрицу по отношению к А ;

· перемножить полученную обратную матрицу с матрицей B .

Простой способ использования Excel для нахождения корней уравнения

Excel – это мощный инструмент, который может использоваться не только для работы с таблицами и вычислений, но и для решения математических задач, например, нахождения корней уравнения. С помощью некоторых функций и формул, доступных в Excel, вы можете легко и быстро найти корни квадратного уравнения.

Чтобы использовать Excel для решения уравнения, вам необходимо знать его коэффициенты. Например, для квадратного уравнения вида ax^2 + bx + c = 0, вы должны знать значения a, b и c. Затем вы можете использовать формулу дискриминанта, чтобы определить количество и тип корней уравнения.

Формула дискриминанта выглядит следующим образом: D = b^2 – 4ac. Если D больше нуля, то у уравнения два различных корня; если D равен нулю, то у уравнения один корень; и если D меньше нуля, то у уравнения нет вещественных корней. В Excel можно использовать функцию SQRT для вычисления квадратного корня.

Для вычисления корней уравнения в Excel вы можете использовать функции IF, AND и OR. Например, если вы хотите найти корни квадратного уравнения, вы можете использовать формулу =IF(AND(D>0, A0), (-B+SQRT(D))/(2*A), IF(AND(D=0, A0), (-B)/(2*A), “”)) для нахождения значений x1 и x2.

Также вы можете использовать таблицы в Excel для нахождения корней уравнений с помощью итерационных методов, таких как метод Ньютона или метод деления пополам. Создайте таблицу с колонками для значений x, f(x) и f'(x), где f(x) – это функция, равная уравнению, а f'(x) – производная функции. Используйте формулу итерации для нахождения следующего значения x и продолжайте итерацию до тех пор, пока значения x не сойдутся к корням уравнения.

Таким образом, Excel предоставляет простой и эффективный способ нахождения корней уравнения. Используйте функции и формулы Excel, чтобы экономить время и упростить процесс решения математических задач.

Решение уравнений методом подбора параметров Excel

Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.

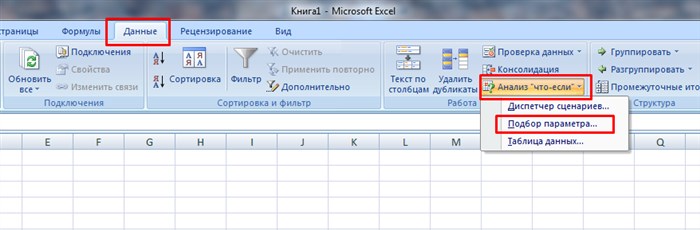
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».

Рассмотрим на примере решение квадратного уравнения х2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:

1. Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
2. Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
3. После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».

Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».

Решение уравнений в excel — примеры решений

Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.

Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».

1. Зададимся простым квадратичным уравнением и найдем решение при х=0.

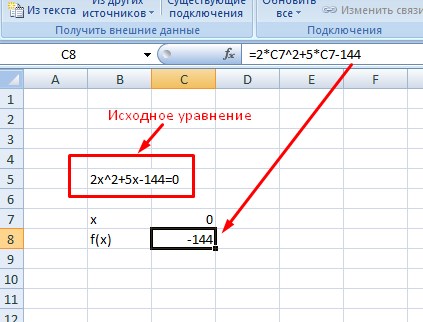
2. Переходите к инструменту и заполняете все необходимые поля

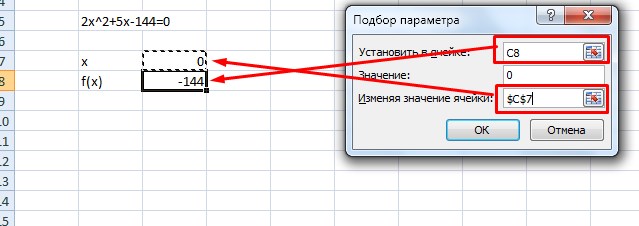
3. После проведения вычислений программа выдаст результат в ячейке с иксом.

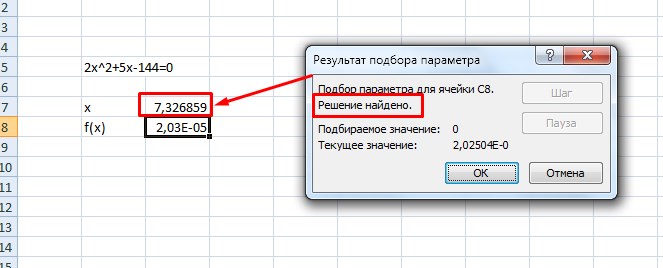
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.

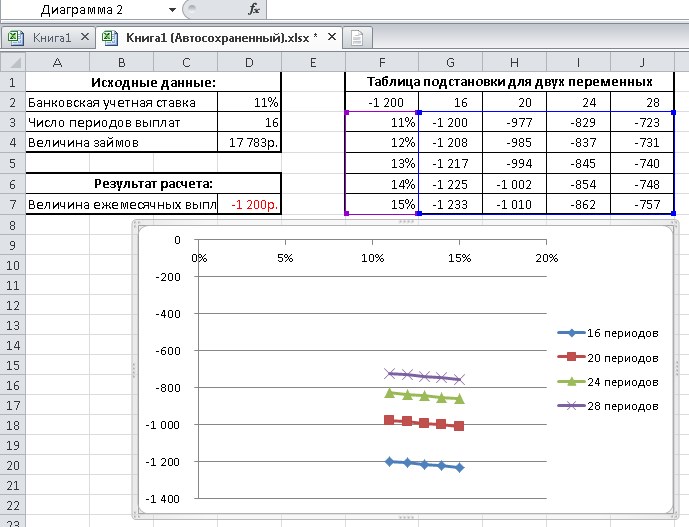
Решение систем уравнений методом Гаусса в Excel

Для примера возьмем простейшую систему уравнений:

3а + 2в – 5с = -12а – в – 3с = 13а + 2в – с = 9

Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.

Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.

1. Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
2. Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
3. Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
4. Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: <=B12:E12/D12>.
5. В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки (<=(B11:E11-B16:E16*D11)/C11>). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты (<=(B10:E10-B15:E15*C10-B16:E16*D10)/B10>). В последнем столбце новой матрицы получаем корни уравнения.

Решение уравнений в Excel

Microsoft Excel предоставляет удобные инструменты для решения математических уравнений. В этой статье мы рассмотрим несколько способов решить уравнения в Excel.

1. Использование встроенных функций:

• Функция SUM — используется для суммирования чисел. Например, для решения уравнения x + 5 = 10, можно записать формулу в ячейке A1: =SUM(10-5)
• Функция IF — позволяет сделать условное вычисление. Например, для решения уравнения 2x + 3 = 9, можно записать формулу в ячейке A1: =IF(2*A1+3=9, A1, «Нет решения»)
• Функция VLOOKUP — используется для поиска значения в диапазоне ячеек. Например, для решения уравнения x^2 + 5 = 30, можно создать таблицу значений и использовать функцию VLOOKUP, чтобы найти корень из 25.

2. Использование инструментов анализа данных:

• Использование данных в столбце для решения уравнения. Например, если у вас есть столбец A с числами и уравнение x + 2 = 10, можно записать в ячейке B1 формулу =10-2, которая автоматически решит уравнение для каждой ячейки в столбце B.
• Использование диаграммы для визуализации решения уравнения. Например, вы можете создать график уравнения и увидеть его точку пересечения с осью x.

3. Использование макросов:

• Создание макроса для решения сложных уравнений. Например, вы можете записать макрос, который будет выполнять итерационные вычисления для решения нелинейных уравнений.
• Использование макроса для автоматического решения уравнений в больших наборах данных. Например, вы можете записать макрос, который будет автоматически применять формулу к большому диапазону ячеек и решать уравнения.

Использование функции SOLVER

Для использования функции SOLVER нужно установить ее в Excel. Для этого откройте программу, перейдите во вкладку «Файл», выберите «Параметры» и далее «Расширение» в левой части окна. Затем найдите «SOLVER» в списке доступных расширений и нажмите «Добавить». После установки функции SOLVER будет доступна в разделе «Анализ» на главной панели Excel.

Чтобы использовать функцию SOLVER, необходимо представить уравнение в виде ячеек Excel. Для этого создайте столбец с переменными, столбец с коэффициентами при переменных и ячейку с целевой функцией, которую нужно минимизировать или максимизировать.

Далее, чтобы настроить и запустить SOLVER, выберите раздел «Анализ» на панели Excel и нажмите на значок SOLVER. В открывшемся окне укажите ячейку с целевой функцией, задайте ограничения на переменные, выберите метод решения и нажмите кнопку «Решить». SOLVER выполнит необходимые вычисления и найдет оптимальное значение переменных, удовлетворяющее заданным ограничениям.

Функция SOLVER также позволяет решать задачи линейного программирования и использовать различные методы оптимизации, такие как методы градиентного спуска или симплекс-метод. Это делает ее очень гибким инструментом для решения различных задач.

Таким образом, использование функции SOLVER в Excel позволяет решать сложные уравнения и оптимизационные задачи, что делает этот инструмент незаменимым для многих пользователей.

Анализ уравнений с помощью графиков

Для решения уравнений в Excel можно использовать мощные инструменты для анализа данных, включая построение графиков. График может быть полезным инструментом для визуализации уравнения и его решений, а также для определения значений переменных в различных точках.

Построение графика уравнения позволяет наглядно представить его поведение и выявить особенности, такие как пересечения с другими линиями, экстремумы или нули. В Excel существует несколько способов создания графиков, включая использование функции «Диаграмма рассеяния» или «График XY».

Чтобы построить график уравнения, необходимо сначала задать значения переменных и вычислить значения функции для каждого набора переменных. Затем эти значения можно представить на графике, где оси соответствуют значениям переменных, а точки отображают значения функции.

Рассмотрим пример построения графика уравнения y = 2x + 3. Для этого можно задать набор значений переменной x и вычислить соответствующие значения функции y. Затем эти значения можно представить на графике.

Построение графика уравнения позволяет визуализировать его решения. Например, можно найти точку пересечения графика с осью x или y, определить значения функции в определенных точках и т. д. Это полезно для анализа уравнений и понимания их свойств.

Таким образом, анализ уравнений с помощью графиков является эффективным инструментом для изучения и понимания математических функций. Excel предлагает широкий выбор инструментов для построения графиков, чтобы помочь вам в анализе уравнений и нахождении их решений.

Расширенные возможности Excel для нахождения корней уравнения

Метод Крамера — вывод формул.

Пусть нам требуется решить систему линейных уравнений вида

Где x 1 , x 2 , …, x n
– неизвестные переменные, a i j
, i = 1, 2, …, n, j = 1, 2, …, n
– числовые коэффициенты, b 1 , b 2 , …, b n
— свободные члены. Решением СЛАУ называется такой набор значений x 1 , x 2 , …, x n
при которых все уравнения системы обращаются в тождества.

В матричном виде эта система может быть записана как A ⋅ X = B
, где — основная матрица системы, ее элементами являются коэффициенты при неизвестных переменных, — матрица – столбец свободных членов, а — матрица – столбец неизвестных переменных. После нахождения неизвестных переменных x 1 , x 2 , …, x n
, матрица становится решением системы уравнений и равенство A ⋅ X = B
обращается в тождество .

Будем считать, что матрица А
– невырожденная, то есть, ее определитель отличен от нуля. В этом случае система линейных алгебраических уравнений имеет единственное решение, которое может быть найдено методом Крамера. (Методы решения систем при разобраны в разделе решение систем линейных алгебраических уравнений).

Метод Крамера основывается на двух свойствах определителя матрицы:

Итак, приступим к нахождению неизвестной переменной x 1
. Для этого умножим обе части первого уравнения системы на А 1 1
, обе части второго уравнения – на А 2 1
, и так далее, обе части n-ого
уравнения – на А n 1
(то есть, уравнения системы умножаем на соответствующие алгебраические дополнения первого столбца матрицы А
):

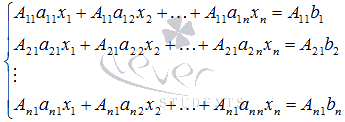
Сложим все левые части уравнения системы, сгруппировав слагаемые при неизвестных переменных x 1 , x 2 , …, x n
, и приравняем эту сумму к сумме всех правых частей уравнений:

Если обратиться к озвученным ранее свойствам определителя, то имеем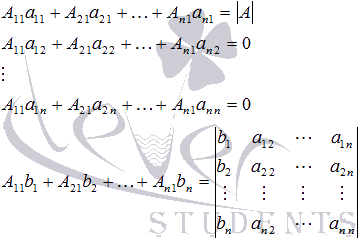
и предыдущее равенство примет вид
откуда

Аналогично находим x 2
. Для этого умножаем обе части уравнений системы на алгебраические дополнения второго столбца матрицы А
:

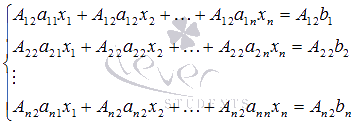
Складываем все уравнения системы, группируем слагаемые при неизвестных переменных x 1 , x 2 , …, x n
и применяем свойства определителя: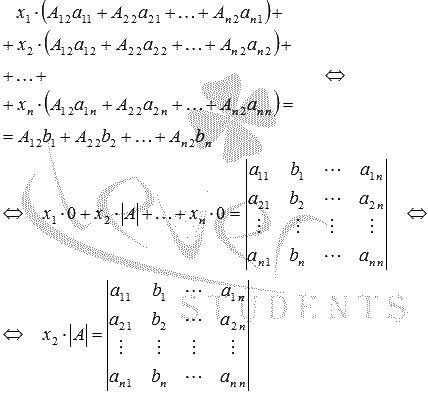

Откуда.

Аналогично находятся оставшиеся неизвестные переменные.

Если обозначить

То получаем формулы для нахождения неизвестных переменных по методу Крамера
.

Замечание.

Если система линейных алгебраических уравнений однородная, то есть , то она имеет лишь тривиальное решение (при ). Действительно, при нулевых свободных членах все определители будут равны нулю, так как будут содержать столбец нулевых элементов. Следовательно, формулы дадут .