Перевод чисел в различные системы счисления с решением

Преобразование десятичной системы счисления в октябрьскую:

Преобразование десятичной дроби в восьмеричную очень похоже на преобразование десятичной дроби в двоичную. Единственная разница заключается в том, что на этот раз мы разделим десятичное число на 8 вместо 2. Преобразование может быть выполнено следующим образом:

Шаг 1: Разделите десятичное число на 8, запишите остаток и присвойте ему значение R1. Аналогично, запишите коэффициент и присвойте ему значение Q1.
Шаг 2: Теперь разделите Q1 на 8, отметьте остаток и коэффициент. Присваиваем значение R2 и Q2 остатку и коэффициенту, полученному на этом шаге.
Шаг 3: Повторяйте последовательность до тех пор, пока не получите значение коэффициента (Qn), равное 0.
Шаг 4: Восьмеричное число будет выглядеть так.: Rn R(n-1) R(n-2) ……………………… R3 R2 R1

Пример: Рассмотрим десятичное число 2181.

2181 / 8 = ( 272 x 8 ) + 5 ………………………………………… R1 = 5 Q1 = 272
272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
34 / 8 = ( 4 x 8 ) + 2 ………………………………………… R3 = 2 Q3 = 4
4 / 8 = ( 0 x 8 ) + 4 ………………………………………… R4 = 4 Q4 = 0

Итак, ОКТАЛЬНЫЙ эквивалент 2181:

(2181) Decimal = (4205) Octal

Нюансы перевода десятичного числа в восьмеричное

При переводе десятичных чисел в восьмеричные системы счисления важно учитывать несколько ключевых моментов. Вот основные из них:. 1

Метод деления: Основной метод перевода включает последовательное деление десятичного числа на 8 и запись остатков. Важно точно выполнять эти деления и правильно записывать остатки

1. Метод деления: Основной метод перевода включает последовательное деление десятичного числа на 8 и запись остатков

Важно точно выполнять эти деления и правильно записывать остатки

2. Порядок остатков: При записи восьмеричного числа остатки читаются в обратном порядке, от последнего к первому. Это часто является источником ошибок.

3. Большие числа: При переводе больших десятичных чисел процесс становится более сложным и требует дополнительной внимательности.

4. Проверка результата: Особенно при ручном переводе рекомендуется проверять полученное восьмеричное число, чтобы убедиться в его правильности.

5. Использование калькулятора: Для упрощения процесса и уменьшения вероятности ошибок рекомендуется использовать онлайн-калькуляторы для перевода.

Практическое применение: Понимание процесса перевода важно в областях, где требуется работа с различными системами счисления, например, в программировании и электронике

Нулевые значения: Ноль в десятичной системе также является нулем в восьмеричной, что важно учитывать при более сложных расчетах

8. Обучение и развитие навыков: Практика перевода чисел из одной системы счисления в другую способствует развитию логического мышления и математических навыков.

9. Вариативность методов: Существуют различные подходы и методы перевода десятичных чисел в восьмеричные, и выбор конкретного метода может зависеть от задачи и личных предпочтений.

10. Двоичная и восьмеричная системы в повседневной жизни: Хотя восьмеричная система может показаться далекой от повседневной жизни, она используется во многих технологиях и электронных устройствах.

Часто задаваемые вопросы о переводе десятичных чисел в восьмеричные

Как правильно перевести большое десятичное число в восьмеричное?

Для перевода больших десятичных чисел в восьмеричные следует использовать метод последовательного деления на 8 и аккуратно записывать остатки в обратном порядке или воспользоваться онлайн-калькулятором для минимизации ошибок.

Можно ли выполнить перевод десятичного числа в восьмеричное вручную?

Да, можно перевести десятичное число в восьмеричное вручную, используя метод последовательного деления на 8 и записи остатков в обратном порядке. Это особенно просто для небольших чисел.

Как обрабатываются ведущие нули в восьмеричном числе?

Ведущие нули в восьмеричном числе (нули перед первой значимой цифрой) не влияют на его значение и могут быть опущены. Однако в некоторых контекстах они могут быть использованы для обозначения определенного количества цифр.

Как проверить правильность перевода десятичного числа в восьмеричное?

Для проверки правильности перевода можно использовать обратный процесс, преобразовывая восьмеричное число обратно в десятичное, или воспользоваться надежным онлайн-калькулятором для сравнения результатов.

Какие особенности нужно учитывать при переводе десятичных чисел в восьмеричные?

При переводе важно точно выполнять деление на 8, внимательно записывать остатки и читать их в обратном порядке. Также следует учитывать, что большие десятичные числа могут требовать более внимательного подхода к переводу

Калькулятор перевода миллиметров в дюймы. Введите длину в миллиметрах для перевода в дюймы.
Калькулятор перевода дюймов в миллиметры. Введите длину в дюймах для перевода в миллиметры.
Калькулятор перевода сантиметров в дюймы. Введите длину в сантиметрах для перевода в дюймы.
Калькулятор перевода дюймов в сантиметры. Введите длину в дюймах для перевода в сантиметры.
Калькулятор перевода систем счисления. Введите число и выберите системы счисления для его перевода.
Калькулятор перевода из шестнадцатеричной в десятичную. Введите шестнадцатеричное число для его перевода в десятичное.
Калькулятор перевода из шестнадцатеричной в двоичную. Введите шестнадцатеричное число для его перевода в двоичное.
Калькулятор перевода из восьмеричной в десятичную. Введите восьмеричное число для его перевода в десятичное.
Калькулятор перевода из восьмеричной в двоичную. Введите восьмеричное число для его перевода в двоичное.
Калькулятор перевода из десятичной в шестнадцатеричную. Введите десятичное число для его перевода в шестнадцатеричное.

Перевод из десятичной системы счисления в восьмеричную

Давайте попробуем изучить перевод десятичного числа в восьмеричное на примере. После этого примера вы без проблем сможете переводить любые числа в эту систему.

Возьмём десятичное число 15 450 и попробуем перевести его в восьмеричную систему счисления.

Для начала нам необходимо разделить исходное число на основание системы, в которую мы хотим это число перевести. Для восьмеричной системы это число 8. То есть мы делим 15 450 на 8.

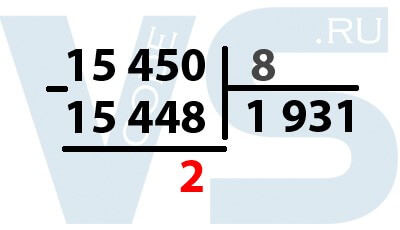
Происходит деление в столбик, но, в отличие от стандартного деления, мы не находим неполные частные, а делим сразу всё делимое на 8. Наибольшим числом, при котором 15 450 делится без остатка на 8 будет число 1 931. 1931 * 8 = 15 448. Теперь мы вычитаем из 15 450 полученное число 15 448, у нас получился остаток 2. Выделяем эту двойку, так как это уже кусочек нашего числа в восьмеричной системе.
Продолжаем: теперь делим полученное на предыдущем шаге частное на 8:

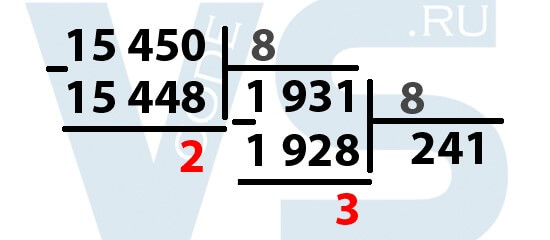
Всё точно так же: наибольшим числом, при котором 1 931 делится без остатка на 8 будет число 241. При умножении 241 на 8 получается число 1 928. Ищем разность между 1 931 и 1928 – получается 3. Выделяем её. Далее делим 241 на 8.

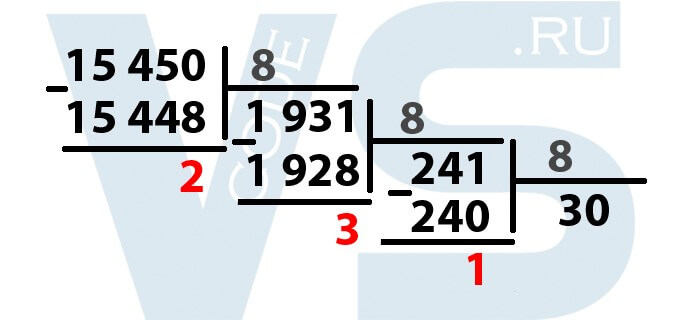
Получается число 30, умножив его на 8, получаем 240. Вычитаем из 241 это число, получается 1. Выделяем единицу.Продолжаем деление до тех пор, пока частное не станет меньше 8!

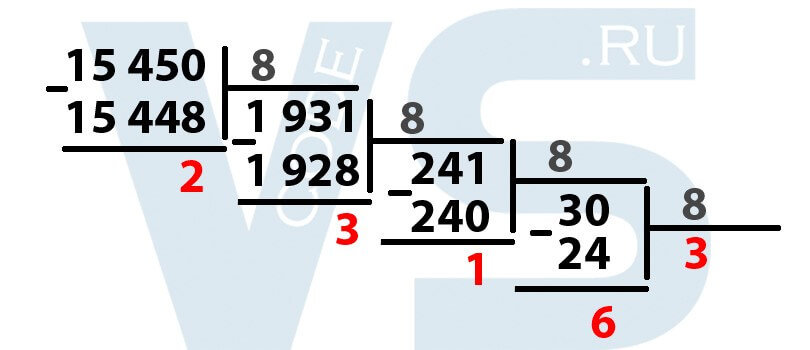Итак, делим 30 на 8, получается 3,75, отбрасываем дробную часть, получается 3. Умножаем 3 на 8, получается 24. 30 — 24 = 6. Выделяем шестёрку. Мы закончили деление так как 3 меньше 8. Обязательно выделяем последнее частное тоже (у нас это цифра 3).

Выделенные красным цифры – это и есть наше число в восьмеричной системе, НО они написаны наоборот. То есть, чтобы правильно прочитать число в восьмеричной системе, необходимо сделать это справа налево.

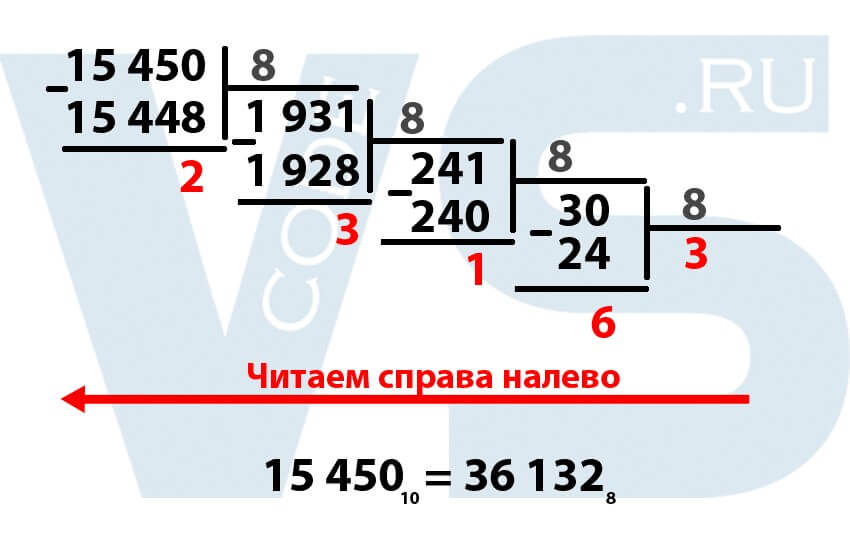
Таким образом, десятичное число 15 450₁₀ в восьмеричной системе будет выглядеть как 36 132₈.

Итого, алгоритм перевода чисел из десятичной системы в восьмеричную следующий:

Разделить исходное число на 8. Найти максимальное частное и убрать дробную часть от него. Например, исходное число 20 : 8 = 2,5. Значит в частное мы записываем число 2.
Умножить полученное частное на 8. Записать его под исходным числом.
Найти остаток между этими числами и выделить его — это кусочек переведённого в восьмеричную систему числа.
Затем разделить в столбик полученное частное на 8, записать ответ и проделать шаги 2 и 3.
Производить деление до тех пор, пока делимое не станет меньше 8. Выделить это делимое тоже.
Выписать все выделенные числа справа налево (т.е. последнее делимое будет на первом месте, затем идёт остаток, найденный на последнем шаге, затем остаток, найденный на предпоследнем шаге и т.д.). Полученное при такой записи число и будет нашим искомым восьмеричным.

Теперь перейдём к переводу восьмеричного числа в десятичную систему счисления.

Какие бывают системы счисления

Наиболее часто используемыми системами счисления являются:

двоичная (2) – все числа записываются лишь посредством двух символов: 0 и 1. Используется в дискретной математике, информатике и программировании.
троичная (3) – числа записываются посредством трёх символов: 0, 1 и 2. Используется в цифровой электронике.
восьмеричная (8) – числа записываются посредством цифр от 0 до 7. Используется в областях связных с цифровыми устройствами, так как восьмеричные числа легко переводятся в двоичные и обратно.
десятеричная (10) – числа записываются посредством цифр от 0 до 9. Используется повсеместно.
двенадцатеричная (12) – числа записываются посредством цифр от 0 до 9 и буквами A и B. Cчёт дюжинами…
шестнадцатеричная (16) – числа записываются посредством цифр от 0 до 9 и буквами A, B, C, D, E, F. Широко используется в программировании и информатике.
двадцатеричная (20) – числа записываются посредством цифр от 0 до 9 и буквами A, B, C, D, E, F, G, H, I (или J), J( или K). Исторически используется во многих языках, в частности в языке йоруба, у тлинкитов, в системе записи чисел майя, некоторых азиатских и кавказских языках.

Обработка ошибок и исключений

При работе с переводом чисел из десятичной системы в восьмеричную в Python, важно учитывать возможность возникновения ошибок и исключительных ситуаций. Некоторые из распространенных ошибок могут включать:

Некорректный ввод данных: Пользователь может ввести недопустимое значение, которое не может быть переведено в восьмеричную систему. Например, ввод строки вместо числа или ввод числа, которое содержит допустимые символы только для десятичной системы.
Переполнение: Если входное число слишком большое, результат восьмеричного представления может превысить допустимый диапазон. В Python, для целых чисел, максимальное значение можно получить с помощью .
Некорректное использование функций: При использовании встроенных функций Python, таких как , необходимо правильно использовать аргументы и учитывать их ограничения. Например, принимает только целые числа.

Для обработки ошибок и исключений в Python, мы можем использовать блок . Внутри блока помещаем код, который может вызвать ошибку, а в блоке указываем, какую ошибку мы хотим обработать и какие действия следует предпринять при возникновении ошибки.

Вот пример, как мы можем обработать ошибки при переводе числа из десятичной системы в восьмеричную:

В этом примере, мы используем функцию для преобразования пользовательского ввода в целое число. Если пользователь вводит некорректные данные (например, строку или число с допустимыми символами только для десятичной системы), возникает исключение . Если входное число превышает максимальное значение для восьмеричного представления, возникает исключение .

Как преобразовать десятичную в восьмеричную

Шаги преобразования:

Разделите число на 8.
Получите целое частное для следующей итерации.
Получите остаток от восьмеричной цифры.
Повторяйте шаги, пока частное не станет равным 0.

Пример №1

Преобразование 7662 ₁₀ в восьмеричное:

Разделение на 8	Частное (целое число)	Остаток (десятичный)	Остаток (восьмеричный)	Цифра #
7662/8	957	6	6
957/8	119	5	5	1
119/8	14	7	7	2
14/8	1	6	6	3
1/8	1	1	4

Итак, 7662· ₁₀ = 16756 _·8.

Пример #2

Преобразование 36631 ₁₀ в восьмеричное:

Разделение на 8	частное	Остаток (десятичный)	Остаток (восьмеричный)	Цифра #
36631/8	4578	7	7
4578/8	572	2	2	1
572/8	71	4	4	2
71/8	8	7	7	3
8/8	1	4
1/8	1	1	5

Итак, 36631 · ₁₀ = 107427· _{8 .}

Пример №3

Преобразование 36731 ₁₀ в восьмеричное:

Разделение на 8	частное	Остаток (десятичный)	Остаток (восьмеричный)	Цифра #
36731/8	4591	3	3
4591/8	573	7	7	1
573/8	71	5	5	2
71/8	8	7	7	3
8/8	1	4
1/8	1	1	5

Итак, 36731· ₁₀ = 107573 _·8.

Применение восьмеричной системы счисления

В прошлом веке выпускались компьютеры, в которых использовались 12-ти, 24-х и 36-битные слова. Это, например, модель ICT 1900 (1964 год), а также PDP-8, выпущенная в 1965 году — это коммерчески довольно успешная модель миникомпьютера в своё время. Кроме того, некоторые мейнфреймы от компании IBM использовали восьмеричную систему. В компьютерах, размер машинного которых кратен тройке, очень удобно использовать систему с основанием восемь, поскольку всегда все биты из слова можно представить в виде целого количества цифр в восьмеричной системе. Например, слово из 24-х бит, можно записать в виде 8-ми восьмеричных чисел.

Если говорить про использование восьмеричной системы в жизни людей, то известно, что в индейских языках Юки (Калифорния) и Паме (Мексика) использовалась данная система. Индейцы считали предметы не по количеству пальцев на руках, а по количеству промежутков между ними.

Поделиться в соц. сетях:

Избранные инструменты:

Калькулятор квадратного корня (высокая точность)конвертер см в футы и дюймыкалькулятор гипотенузыфуты дюймы в сантиметрыКалькулятор относительного стандартного отклонения (Высокая точность)Генератор случайных цветовкалькулятор дисперсии (Высокая точность)Шестнадцатеричный калькуляторпобитовый калькуляторКалькулятор модулякалькулятор жима лежаслучайный выборКалькулятор коэффициентов и процентовконвертер фунтов в кгКалькулятор дня годаКалькулятор числа судьбыконвертер кг в фунтыдвоичный калькуляторгенератор случайных строквосьмеричный калькуляторкалькулятор десятичной дробикалькулятор стандартных ошибок (Высокая точность)Калькулятор выборки среднегоГенератор MAC-адресовКалькулятор стандартного отклонения выборкиНумерологический калькуляторкалькулятор рентабельности продажКалькулятор валовой прибыликалькулятор годовыхКалькулятор инфляции в СШАкалькулятор натуральных логарифмовКалькулятор теоремы Пифагоравыбор случайного имениКалькулятор чистой прибылиКонвертер римских цифркалькулятор коэффициента дисконтаКалькулятор функции ошибкиПреобразователь двоичного кода в код Греяпреобразователь сахара в кровиКалькулятор соотношения талии и бедерКалькулятор АНКпреобразователь обычного времени в десятичное времяСортировка номеровКалькулятор EBITDAСписок чисел ФибоначчиКалькулятор контрольной суммы CRC32HbA1c калькуляторКалькулятор бета-функциисчетверенный калькуляторCAGR калькуляторкалькулятор суммы последовательных чиселкалькулятор процентной ошибкиКалькулятор коэффициента вариацииКалькулятор дополнительной функции ошибкиКонвертер десятичных чисел в BCDкалькулятор числа жизненного путикалькулятор диапазонакалькулятор среднего отклоненияHEX конвертерКалькулятор гамма-функциикалькулятор комиссиигенератор случайных буквКод Грея в двоичный преобразователькалькулятор золотого сеченияконвертер размера файлаКалькулятор WACCкалькулятор золотого прямоугольникаКонвертер PPM в процентыКонвертер дробей в процентахAPY to APR калькуляторКалькулятор межквартильного диапазонакалькулятор суммы квадратовКалькулятор ПВИФ (Высокая точность)Двоичный в шестнадцатеричный конвертерIPv4/IPv6 в двоичный конвертерКалькулятор WHTRкалькулятор биномиального коэффициентаКалькулятор среднеквадратичного значениякалькулятор общего множителявыбор случайных чиселГенератор GUID/UUIDКалькулятор эквивалентной дробиКалькулятор среднего абсолютного отклоненияКалькулятор одного повторного максимума (1ПМ)Калькулятор периметра эллипсаКалькулятор доходности облигацийкалькулятор числа личностиКонвертер процентов в PPMКалькулятор цены за тысячу показовКакое у меня счастливое число?Калькулятор среднего среднего режимаКалькулятор отношения BUN к креатининуГенератор случайных английских цитатКонвертер BCD в десятичные числаКалькулятор кинематикиДекодер азбуки МорзеКонвертер десятичных чисел в экспоненциальныеГенератор азбуки МорзеКонвертер двоичного кода в BCDмедианный калькуляторКонвертер десятичного числа в восьмеричное

Конвертер из десятичной в восьмеричную систему: бесплатный онлайн инструмент

Конвертер из десятичной в восьмеричную систему — это онлайн-инструмент, который помогает пользователям преобразовывать десятичные числа в их соответствующие восьмеричные числа. Этот бесплатный инструмент доступен онлайн и не требует никаких системных или программных зависимостей. Он прост в использовании и безопасен, обеспечивая безопасность данных и возможность локальных вычислений.

Особенности конвертера из десятичной в восьмеричную систему

Онлайн и бесплатное использование, без системных и программных зависимостей
Возможность очистить, скопировать, пример
Безопасность данных, локальные вычисления

Как использовать конвертер из десятичной в восьмеричную систему

Использование конвертера из десятичной в восьмеричную систему просто и понятно. Вот шаги, которые нужно выполнить:

Введите или вставьте ваше десятичное число в предоставленное поле ввода.
Нажмите кнопку «Преобразовать», чтобы преобразовать десятичное число в его восьмеричный эквивалент.
Скопируйте восьмеричное число или нажмите кнопку «Скопировать», чтобы скопировать его в буфер обмена.
Чтобы очистить поле ввода, нажмите кнопку «Очистить».
Вы также можете использовать опцию «Пример», чтобы попробовать инструмент с предварительно заполненным десятичным числом.

Преимущества использования конвертера из десятичной в восьмеричную систему

Использование конвертера из десятичной в восьмеричную систему предоставляет несколько преимуществ для пользователей:

Это онлайн-инструмент, который не требует загрузки какого-либо программного обеспечения для использования.
Инструмент прост и понятен, обеспечивая простой и интуитивно понятный интерфейс.
Он безопасен и обеспечивает безопасность данных, вычисляя данные локально.
Инструмент предоставляет удобство быстрого и легкого преобразования десятичных чисел в восьмеричные без каких-либо зависимостей или предварительных условий.

Основной алгоритм или логика

Основной алгоритм, используемый конвертером из десятичной в восьмеричную систему, основан на делении десятичного числа на 8 повторно до тех пор, пока частное не будет равно нулю. На каждом шаге остаток записывается и объединяется, чтобы сформировать восьмеричное число. Формула для алгоритма выглядит следующим образом:

PHP Code:

Конвертер из десятичной в восьмеричную систему — это простой и удобный онлайн-инструмент, который позволяет быстро и легко преобразовывать десятичные числа в восьмеричные числа. Он безопасен и бесплатен, обеспечивая безопасность данных и возможности локального вычисления. Основным алгоритмом, используемым инструментом, является деление десятичного числа на 8 повторно и запись остатка на каждом шаге. С помощью этого инструмента вы легко можете преобразовывать десятичные числа в восьмеричные с использованием Python, C, JavaScript, Java и PHP.

Перевод из десятичной в двоичную, восьмеричную и шестнадцатеричную системы

Для того что бы перевести из десятичной системы в любую другую необходимо последовательно делить число на основание той системы в которую переводим до тех пор пока частное от деления не станет равным нулю. Далее записываем остатки от делений в обратном порядке. Полученная последовательность будет являться результатом перевода в выбранную систему счисления. Для понимания указанных действий разберем последовательное преобразование для каждой из систем.

Из десятичной в двоичную. Исходное число 230, основание системы «2». Производим последовательное деление:

230 ÷ 2 = 115 (в остатке );
115 ÷ 2 = 57 (в остатке 1);
57 ÷ 2 = 28 (в остатке 1);
28 ÷ 2 = 14 (в остатке );
14 ÷ 2 = 7 (в остатке );
7 ÷ 2 = 3 (в остатке 1);
3 ÷ 2 = 1 (в остатке 1);
1 ÷ 2 = 0 (в остатке 1).

Записываем остатки от деления на 2 в обратном порядке и получаем следующую последовательность: 11100110. Полученный результат является двоичным представлением числа 230.

Из десятичной в восьмеричную. Исходное число 789, основание системы «8». Производим последовательное деление:

789 ÷ 8 = 98 (в остатке 5);
98 ÷ 8 = 12 (в остатке 2);
12 ÷ 8 = 1 (в остатке 4);
1 ÷ 8 = 0 (в остатке 1).

Записываем остатки от деления на 8 в обратном порядке и получаем следующую последовательность: 1425. Полученный результат является восьмеричным представлением числа 789.

Из десятичной в шестнадцатеричную. Исходное число 7000, основание системы «16». Производим последовательное деление:

7000 ÷ 16 = 437 (в остатке 8);
437 ÷ 16 = 27 (в остатке 5);
27 ÷ 16 = 1 (в остатке 11);
1 ÷ 16 = 0 (в остатке 1).

Записываем остатки от деления на 16 в обратном порядке. Если остаток от деления больше 9, то вместо числа записываем букву, соответствие чисел и букв представлено ниже в таблице. В результате получаем следующую последовательность: 1B58. Полученный последовательность является шестнадцатеричным представлением числа 7000.

число	буква
10	A
11	B
12	C
13	D
14	E
15	F

Примеры перевода чисел

Давайте рассмотрим несколько примеров перевода чисел, чтобы лучше понять процесс.

Пример 1. Представьте, вы хотите похвастаться перед друзьями, зная свой вес в двоичной системе. Если ваш вес 70 кг, то в двоичной системе это будет 1000110. Не забудьте уточнить, что это в килограммах, а не в тоннах!

Пример 2. Ваш друг говорит, что его новая машина стоит ‘1010000’ в некой таинственной системе. Вы быстро переводите и понимаете, что это 80 в десятичной системе. Надеемся, это стоимость в тысячах!

Пример 3. Вас попросили принести ‘100’ пирожных на вечеринку. Чтобы удивить всех, вы переводите это в шестнадцатеричную систему и приносите 256 пирожных. Ваша популярность на вечеринке гарантирована (или нет).

Системы счисления простым языком

Системы счисления — это способы записи чисел, которые мы используем в повседневной жизни. Подумайте о них как о разных языках для цифр. Как и в языках, где у нас есть разные слова для обозначения одного и того же предмета, в разных системах счисления одно и то же число может выглядеть по-разному.

Каждая система счисления имеет своё «основание», которое определяет количество используемых символов. Например, в десятичной системе, которой мы пользуемся каждый день, основание равно 10, потому что у нас есть 10 разных цифр (от 0 до 9). Системы счисления нужны нам для разных задач: от счета денег и измерения времени до программирования компьютеров и шифрования информации.

Кроме десятичной, существуют и другие системы, например, двоичная, которую любят компьютеры, восьмеричная и шестнадцатеричная, часто используемые в программировании. Различные системы счисления позволяют нам более эффективно решать определенные задачи, такие как обработка данных в компьютере или представление больших чисел более компактно.

Десятичная система (Base 10)

Это система, которую мы используем каждый день. Она основана на 10 цифрах от 0 до 9. Каждая позиция в числе имеет значение, увеличивающееся в 10 раз с каждым шагом влево. Например, в числе 345, 5 — это единицы, 4 — десятки, а 3 — сотни.

Пример: 123 в десятичной системе означает 1×100 + 2×10 + 3×1.

Двоичная или бинарная система (Base 2)

Двоичная система использует только две цифры: 0 и 1. Каждая позиция в числе увеличивает своё значение в 2 раза с каждым шагом влево. Эта система широко используется в компьютерных технологиях.

Пример: 101 в двоичной системе означает 1×4 + 0×2 + 1×1, что равно 5 в десятичной системе.

Восьмеричная система (Base

Восьмеричная система использует цифры от 0 до 7. Каждая позиция в числе увеличивается в 8 раз с каждым шагом влево. Эта система иногда используется в программировании.

Пример: 234 в восьмеричной системе означает 2×64 + 3×8 + 4×1, что равно 156 в десятичной системе.

Шестнадцатеричная система (Base 16)

Шестнадцатеричная система использует 16 символов: цифры от 0 до 9 и буквы от A до F. Каждая позиция увеличивается в 16 раз с каждым шагом влево. Эта система часто применяется в информатике и программировании.

Пример: 1A3 в шестнадцатеричной системе означает 1×256 + A(10)×16 + 3×1, что равно 419 в десятичной системе.

История возникновения систем счисления

История систем счисления уходит корнями в глубокую древность. Самые ранние системы счисления были созданы для удовлетворения базовых потребностей в счете и измерении. Например, древние люди использовали примитивные методы, такие как камешки или зарубки на палках, для подсчета предметов.

Одной из первых разработанных систем счисления считается вавилонская, возникшая около 2000 года до н.э. Она была позиционной и использовала основание 60, что до сих пор отражается в нашем измерении времени (60 секунд в минуте, 60 минут в часе).

Древние египтяне разработали свою систему счисления примерно в 3000 году до н.э. Эта система была десятичной, но непозиционной, что означает использование отдельных иероглифов для обозначения единиц, десятков, сотен и так далее.

Двоичная система, которая лежит в основе современных компьютерных технологий, была впервые полноценно описана в работах Готфрида Лейбница в 17-м веке, хотя подобные идеи возникали и ранее

Лейбниц понимал важность двоичной системы для развития математики и науки

Восьмеричная и шестнадцатеричная системы, хотя и использовались в различных культурах на протяжении истории, получили широкое распространение в эпоху развития компьютерных технологий, поскольку они представляют собой компактную форму двоичного кода, удобную для человеческого восприятия.

Таким образом, различные системы счисления развивались в разных культурах в ответ на практические потребности и математические исследования, формируя основу для наших современных числовых представлений и вычислительных технологий.

Перевод из двоичной системы в шестнадцатеричную и обратно

Для начала необходимо разбить двоичное число на группы по 4 символа (цифры). Каждой группе необходимо сопоставить её шестнадцатеричное значение, указанное в таблице.

значение₂	значение₁₆
0000
0001	1
0010	2
0011	3
0100	4
0101	5
0110	6
0111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

Пример. Переведем двоичное число 111010 в шестнадцатеричное. Для начала разделим его на группы по 4 цифры, предварительно дописав нули с левой стороны, для того чтобы количество цифр в исходном числе стало кратно 4: 0011 1010. Находим соответствие каждой группе в таблице и получаем для первой группы — 3, для второй группы — A. Получаем конечный результат — 3A.

Для перевода из шестнадцатеричного системы в двоичную необходимо произвести все действия в обратном порядке.

Пример. Переведем число 1A4D в двоичное. Находим соответствие каждому символу его двоичное значение в таблице. Символу 1 соответствует 0001, символу A — 1010, символу 4 — 0100, символу D — 1101. Запишем полученные значения в соответствующем порядке: 0001 1010 0100 1101. Нули с левой стороны числа можно убрать, так как они не являются значимыми: 1101001001101.