Размещения
Пусть в футбольном турнире участвуют 6 команд. Нам предлагают угадать те команды, которые займут призовые места (то есть первые три места). Сколько вариантов таких троек существует?
Сначала запишем ту команду, которая выиграет турнир. Здесь есть шесть вариантов, по количеству участвующих команд. Запишем эти варианты:

Далее выберем один из вариантов и для него укажем серебряного призера соревнований. Здесь есть только 5 вариантов, ведь 1 из 6 команд уже записана на 1-ом месте:

Такую пятерку можно записать для каждого из шести вариантов того, кто станет чемпионом. Получается, что всего есть 6•5 = 30 пар «чемпион – серебряный призер». Наконец, для одной такой пары можно записать 4 варианта того, кто окажется третьим (две команды писать нельзя, так как они уже записаны на первых двух строчках):

Для каждой пары можно записать 4 тройки призеров. Так как число пар «чемпион – вице-чемпион» равно 6•5 = 30, то число троек составит 6•5•4 = 120.
В данном случае из некоторого множества команд мы выбрали несколько и расположили их в каком-то порядке. То есть мы выбрали упорядоченное множество. В комбинаторике оно называется размещением.

Если общее число команд обозначить как n (в этом примере n = 6), а количество упорядочиваемых команд равно k, то количество таких размещений в комбинаторике обозначается как
В примере с командами количество размещений равнялось 120:
Читается эта запись как «число размещений из 6 по 3 равно 120».
Для нахождения этого числа мы перемножили k (3)множителей. Первый из них был равен n(6), так как каждая из n команд могла занять первая место. Второй множитель был равен (n– 1), так как после определения чемпиона мы могли поставить на вторую позицию одну из (n– 1) команд. Третий множитель был равен (n– 2). По этой логике каждый следующий множитель будет меньше предыдущего на единицу. Например, чтобы вычислить число размещений из 7 по 4, надо перемножить 4 множителя, первый из которых равен 7, а каждый следующий меньше на 1:
Однако математически удобнее представлять это произведение как отношение двух факториалов. Для этого умножим количество размещений на дробь 3!/3!, равную единице. Естественно, число размещений из-за умножения на единицу не меняется:
![]()
Число 3 в данном случае можно получить, если из 7 вычесть 4. В общем случае из числа n надо вычесть число k. Тогда формула для вычисления количества размещений примет вид:

Пример. В программе 8 «А» класса 12 различных предметов. В понедельник проводится 5 занятий подряд. Сколько существует вариантов расписаний для класса, если в течение понедельника нельзя проводить два одинаковых урока?
Решение. Для составления расписания нужно выбрать 5 предметов и расставить их по порядку. Поэтому нам необходимо найти размещение из 12 по 5:

Ответ: 95040
Пример. В вагоне 10 свободных мест. В него зашло 6 пассажиров. Сколькими способами они могут расположиться в вагоне?
Решение. Из десяти мест надо выбрать шесть и указать для каждого, какому пассажиру оно соответствует. То есть каждый вариант рассадки пассажиров – это размещение из 10 по 6. Найдем их количество:

Ответ: 151200
Заметим, что перестановка – это частный случай размещения, когда k = n. Действительно, если нам надо указать тройку призеров турнира, в котором участвуют 6 команд, то мы указываем размещение из 6 по 3. Но если мы указываем для каждой из 6 команд, какое место она займет в чемпионате, то это размещение из 6 по 6. С другой стороны, это расстановка одновременно является и перестановкой 6 команд. Убедимся, что в этом частном случае формула для подсчета количества размещений покажет тот же результат, что и формула для перестановок
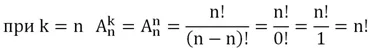
Для примера с 6 командами это будет выглядеть так:
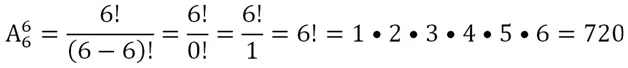
Здесь мы использовали тот факт, что факториал нуля принимается равным единице. Данное рассуждение можно, наоборот, использовать для того, чтобы доказать, что факториал нуля – это единица.
Сочетания
Выбирая размещение, мы должны были выбрать из множества несколько объектов и упорядочить их. В частности, мы выбирали три команды из шести и указывали, какая из них будет первой, какая второй, а какая третьей. Поэтому размещения «Локомотив, Зенит, Краснодар» и «Локомотив, Краснодар, Зенит» отличались друг от друга.
Однако порою этот порядок не имеет значения. Так, существует известная лотерея, где предлагается угадать 7 чисел из 49, которые выпадут во время розыгрыша из барабана. При этом порядок их выпадения не играет никакой роли. Игрок, выбирая эти 7 чисел, с точки зрения математики формирует сочетание из 49 по 7.

Количество возможных сочетаний из n по k обозначается буквой С:
Для вычисления количеств сочетаний из n по k сначала найдем количество аналогичных размещений. Оно вычисляется по формуле:
Однако ясно, что, как и в случае с перестановками с повторениями, некоторые сочетания мы посчитали несколько раз. Вернемся к примеру с командами. Если мы выбрали команды Л (Локомотив) , З (Зенит) и К (Краснодар), то мы можем составить ровно 3! = 6 размещений из них:
ЛЗК
ЛКЗ
ЗЛК
ЗКЛ
КЛЗ
КЗЛ
Однако все они соответствуют только одному сочетании – ЛКЗ. Таким образом, считая количество размещений, мы посчитали каждое сочетание не один, а 3! раз. Поэтому для нахождения количества сочетаний в комбинаторике надо поделить число размещений на число перестановок k элементов:
Эта формула связывает важнейшие понятия комбинаторики – перестановки, сочетания и размещения. Подставим в неё формулы для размещений и перестановок и получим:
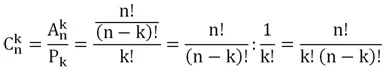
Пример. Сколько троек призеров турнира можно составить, выбирая три футбольные команды из шести?
Решение. Посчитаем число сочетаний из 6 по 3:
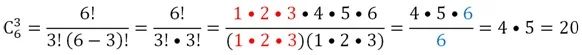
Ответ: 20
Пример. Сколько комбинаций чисел может составить игрок, играющий в лотереи «5 из 36», «6 из 45», «7 из 49»?
Решение. В каждом из этих случаев игрок выбирает сочетание нескольких чисел. Посчитаем их число:

Ответ: 376992; 8145060; 85900584
Пример. На плоскости отмечены 8 точек, причем никакие три из них не лежат на одной прямой. Сколько различных прямых можно провести через них? Сколько треугольников и четырехугольников можно построить с вершинами в этих точках?
Решение. Для того чтобы провести прямую, достаточно выбрать любые 2 точки из 8. Общее количество прямых будет равно числу сочетаний из 8 по 2:
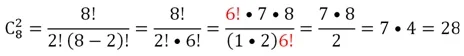
Заметим принципиальную важность того условия, что никакие три точки не лежат на одной прямой. Оно гарантирует, что при выборе двух различных точек мы будем получать различные прямые
Если бы, например, точки АВС лежали бы на одной прямой, то при выборе сочетаний АВ, ВС и АС мы получали бы одну и ту же прямую:
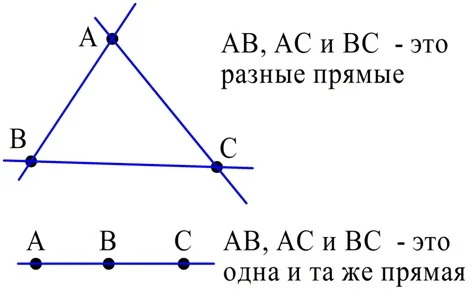
Это же условие гарантирует, что, выбрав любые 3 и 8 точек, мы сможем построить треугольник с вершинами в этих точках, а выбрав 4 точки, получим четырехугольник. Поэтому для подсчета количества треугольников и четырехугольников следует искать число сочетаний по 3 и 4:
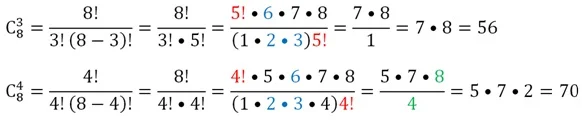
Ответ: 28 прямых, 56 треугольников и 70 четырехугольников.
Пример. В одной урне находится 10 различных шаров с номерами от 0 до 9, а в другой – 8 различных шаров с первыми восемью буквами алфавита. По условиям лотереи ведущий вытаскивает из первой урны два шара с числами, а из второй – три шара с буквами. Для победы в лотерее надо угадать выпавшие шары. Сколько комбинаций шаров может выпасть в игре?
Решение. Посчитаем отдельно, сколькими способами можно выбрать 2 шара с цифрами из 10 и 3 шара с буквами из 8:

По правилу умножения мы должны перемножить эти числа, чтобы найти общее количество возможных вариантов:
56•45 = 2520
Ответ: 2520
Заметим, что выбирая, например, сочетание из 49 по 7, мы одновременно выбираем и сочетание из 49 по 49 – 7 = 42. Действительно, игрок, обводящий в кружок в лотерейном билете свои 7 счастливых чисел, одновременно и определяет остальные 42 числа, какие числа он НЕ считает счастливыми. Для наглядности запишем число сочетаний в обоих случаях:
Получили одну и ту же дробь, в которой отличается лишь последовательность множителей в знаменателе. Можно показать, что и в общем случае число сочетаний из n по k совпадает с количеством сочетаний из n по (n– k):
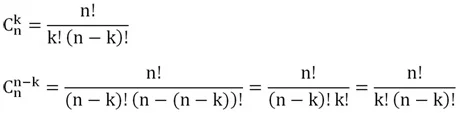
Источники
Список источников, которые использовались при написании темы.
Для более глубокого погружения в материал рекомендуем ознакомиться с ними подробнее:
Комбинаторика
Виленкин Н.Я., Виленкин А.Н., Виленкин П.А., 7-е издание, МЦНМО, 2019
Почти идеальная подача теории через жизненные примеры. Интересные задачи. Широчайший охват тем, в том числе и из высшей математики.
5. Размещения с повторениями
6. Секретный замок
7. Системы счисления и передача информации
8. Вокруг ЭВМ
9. Морской семафор
10. Точки—тире телеграфные
18. Первенство по футболу
19. Размещения без повторений
Википедия
Свободная энциклопедия
Оптический телеграф
Optical telegraph
Chappe telegraph
Telegraph code
Азбука Морзе
Композиция числа
Сочетания
Рассмотрим задачу, аналогичную задаче 5, но с существенным отличием.
7. Сколько существует различных вариантов выбора 4-х кандидатур из 9-ти специалистов?
В этой задаче нам нужно выбрать 4 кандидатуры, но при этом не важно, в каком порядке мы их выбираем, нас интересует только состав выбранных элементов, но не порядок их расположения. Если бы нас интересовал порядок расположения элементов, как в задаче 5, то мы могли применили бы формулу для нахождения числа размещений из 9 по 4:
Если бы нас интересовал порядок расположения элементов, как в задаче 5, то мы могли применили бы формулу для нахождения числа размещений из 9 по 4:
4 различных элемента можно расположить в определенном порядке 4! различными способами. Поскольку нас не интересует порядок расположения элементов, число способов, которыми мы можем выбрать 4 элемента, не располагая их в определенном порядке, уменьшается в 4! раза по сравнению с предыдущей задачей (так как для данной задачи различное расположение данных элементов считается одним способом), и мы получаем
способов.
В этой задаче появляется понятие сочетания.
Сочетаниями из n элементов по k элементов называются подмножества, состоящие из k элементов множества (множества, состоящего из n элементов).
Внимание! Одно сочетание от другого отличается только составом выбранных элементов (но не порядком их расположения, как у размещений). Число сочетаний из n элементов по k элементов обозначается
Число сочетаний из n элементов по k элементов обозначается
и находится по формуле:
Число сочетаний из n по k показывает, сколькими способами мы можем выбрать k элементов из n элементов, или сколькими способами мы можем расположить k объектов по n местам.
Легко заметить, что
8. В коробке лежат 8 красных карандашей и 4 синих. Из коробки наугад вынимают 4 карандаша. Какова вероятность того, что среди них окажется 2 красных и 2 синих?
Решение.
Вопросы
- Вычислите результат целочисленного деления.23 // 7 = 320 // 5 = 42 // 5 = 0123 // 10 = 12— 123 // 10 = -13
- Вычислите остаток от деления.23 % 7 = 220 % 5 = 02 % 5 = 2123 % 10 = 3
- Что будет выведено на экран в результате выполнения следующей программы?a = 15 // (16 % 7) b = 34 % a * 5 — 29 % 5 * 2 print(a + b)Ответ: 29
- Что будет выведено на экран в результате выполнения следующей программы?a = 82 // 3 ** 2 % 7print(a)Ответ: 2
# Получаем переменные b1,q,n b1 = int(input()) q = int(input()) n = int(input()) # Выводим результат на экран print(b1 * q ** (n-1))
# Получаем число в сантиметрах и записываем в переменую cm cm = int(input()) # Переводим сантиметры в метры m = cm // 100 # Выводим результат на экран print(m)
# Получаем число школьников и мандаринов записав данные в переменные sch = int(input()) fru = int(input()) # Выводим результат на экран print(fru // sch) print(fru % sch)
# Получаем население и записываем в переменную n n = int(input()) # Выводим на экран колличество выживших print(n//2 + n%2)
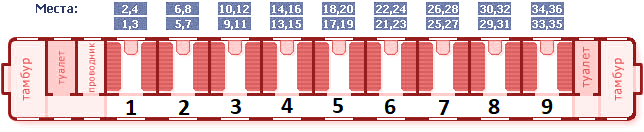
# Получаем номер места и кладем в переменную n n = int(input()) # Добавленное к месту 3 оставшихся места и проводим целочисленное деление на количество мест в купе (4) print((n + 3) // 4)
# Получаем и записываем в переменную кол-во минут m = int(input()) h = m // 60 # Часы целочисленное деление s = m % 60 # Минуты остаток от деления # Выводим результат на экран print(m, "мин - это", h, "час", s, "минут.")
# Получаем число и сохраняем в переменную num
num = int(input())
a = num % 10 # Последняя цифра числа
b = (num % 100) // 10 # Предпоследняя цифра числа
c = num // 100 # Первая цифра числа
# Выводим результат на экран
print("Сумма цифр =", c + b + a)
print("Произведение цифр =", c * b * a)
# Получаем трехзначное число и сохраняем в переменную abc abc = int(input()) c = abc % 10 # Последняя цифра числа b = (abc % 100) // 10 # Предпоследняя цифра числа a = abc // 100 # Первая цифра числа # Выводим перебор всех перестановок цифр print(a, b, c, sep='') print(a, c, b, sep='') print(b, a, c, sep='') print(b, c, a, sep='') print(c, a, b, sep='') print(c, b, a, sep='')
# Получаем число и сохраняем в m
m = int(input())
m1 = m // 1000 # Цифра в позиции тысяч
m2 = (m // 100) % 10 # Цифра в позиции сотен
m3 = (m // 10) % 10 # Цифра в позиции десятков
m4 = m % 10 # Цифра в позиции единиц
# Выводим результат согласно условиям
print("Цифра в позиции тысяч равна", m1)
print("Цифра в позиции сотен равна", m2)
print("Цифра в позиции десятков равна", m3)
print("Цифра в позиции единиц равна", m4)

Следующий модуль 3: Итоговая работа по условным операторам («Поколение Python»).
Расчет комбинаций с повторениями
Комбинации с повторениями – это комбинации, в которых элементы могут повторяться. В контексте паролей это означает, что все шесть цифр могут быть одинаковыми, а также некоторые из них могут повторяться.
Для расчета количества комбинаций с повторениями используется простая формула: количество возможных значений возведенное в степень количества элементов.
Для шестизначного пароля из цифр (0-9) количество возможных значений равно 10 (так как 0 считается допустимым значением). Поэтому формула будет выглядеть следующим образом: 10 в степени 6.
Чтобы рассчитать результат, необходимо выполнить возведение в степень. В данном случае:
10 в степени 6 = 10 × 10 × 10 × 10 × 10 × 10 = 1 000 000
Таким образом, у шестизначного пароля из цифр возможно 1 000 000 комбинаций с повторениями.
Сколько всего комбинаций из 6 цифр?
Для определения количества возможных комбинаций из 6 цифр необходимо учесть, что каждая позиция может принимать значения от 0 до 9 (так как мы имеем дело с цифрами).
Таким образом, для первой позиции у нас имеется 10 вариантов (0-9), для второй позиции также 10 вариантов, и так далее до шестой позиции. Чтобы найти общее количество комбинаций, необходимо перемножить количество вариантов для каждой позиции:
- 10 вариантов для первой позиции
- 10 вариантов для второй позиции
- 10 вариантов для третьей позиции
- 10 вариантов для четвертой позиции
- 10 вариантов для пятой позиции
- 10 вариантов для шестой позиции
Итак, общее количество комбинаций равно произведению количества вариантов для каждой позиции:
10 * 10 * 10 * 10 * 10 * 10 = 1,000,000
Таким образом, всего существует 1,000,000 (один миллион) возможных комбинаций из 6 цифр.
Каково возможное количество комбинаций из 6 цифр?
Вопрос о количестве возможных комбинаций из 6 цифр может быть важным, когда речь идет о создании паролей, шифровании данных или других ситуациях, требующих случайного выбора. Чтобы определить количество комбинаций, необходимо знать количество возможных значений для каждой цифры и количество позиций, которые могут занимать цифры.
Для шестизначного числа возможные значения для каждой позиции — это числа от 0 до 9. Таким образом, каждая позиция может принять 10 возможных значений (0-9).
Чтобы найти общее количество комбинаций, необходимо умножить количество возможных значений каждой позиции на количество позиций в числе. В данном случае, общее количество комбинаций равно 10^6.
10^6 — это математическая запись для степени числа 10. Это значит, что нужно умножить число 10 на само себя 6 раз. В результате получается 1 000 000 возможных комбинаций.
Таким образом, возможное количество комбинаций из 6 цифр равно 1 000 000.
Как быстро рассчитать все комбинации из 6 цифр?
Рассчитать все возможные комбинации из 6 цифр может оказаться нетривиальной задачей. Однако с помощью математических формул и методов, можно достичь этой цели. Один из способов рассчитать все комбинации состоит в использовании перестановок и сочетаний.
Перестановка — это упорядоченное расположение элементов множества. Для нахождения всех перестановок из 6 цифр можно воспользоваться формулой:
n! / (n — r)!
где n — общее количество элементов (в данном случае 10 цифр), а r — количество выбираемых элементов (в данном случае 6 цифр).
Сочетание — это неупорядоченный выбор элементов множества. Для нахождения всех сочетаний из 6 цифр можно воспользоваться формулой:
n! / (r! * (n — r)!)
где n и r имеют те же значения, что и в формуле для перестановок.
Например, для нахождения всех комбинаций из 6 цифр можно использовать следующий код на языке Python:
from itertools import combinations digits = combinations = list(combinations(digits, 6)) print(combinations)
В данном примере мы используем функцию combinations из модуля itertools, чтобы получить все возможные сочетания из списка цифр digits. Результат будет выведен в виде списка комбинаций.
- Количество перестановок из 6 цифр: 120
- Количество сочетаний из 6 цифр: 210
Таким образом, с помощью математических формул и программ кода, можно быстро рассчитать все комбинации из 6 цифр. Это может быть полезно для различных задач, таких как генерация паролей, перебор возможных комбинаций и других подобных случаев.
Перестановки из n элементов
Определение 3. Перестановкой
из n
элементов
называется любой упорядоченный набор
этих элементов.
Пример 7a.
Всевозможными перестановками
множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3,
2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).
Число различных перестановок из n элементов обозначается P n и
вычисляется по формуле P n =n!.
Пример 8.
Сколькими способами семь книг
разных авторов можно расставить на полке в один ряд?
Решение:
эта задача о числе
перестановок семи разных книг. Имеется P 7 =7!=1*2*3*4*5*6*7=5040
способов осуществить расстановку книг.
Обсуждение.
Мы видим,
что число возможных комбинаций можно посчитать по разным правилам
(перестановки, сочетания, размещения) причем результат получится различный,
т.к. принцип подсчета и сами формулы отличаются. Внимательно посмотрев на
определения, можно заметить, что результат зависит от нескольких факторов
одновременно.
Во-первых, от того, из какого количества элементов мы можем комбинировать их
наборы (насколько велика генеральная совокупность элементов).
Во-вторых, результат зависит от того, какой величины наборы элементов нам
нужны.
И последнее, важно знать, является ли для нас
существенным порядок элементов в наборе. Поясним последний фактор на
следующем примере
Пример 9.
На родительском собрании
присутствует 20 человек. Сколько существует различных вариантов состава
родительского комитета, если в него должны войти 5 человек?Решение:
В этом примере нас
не интересует порядок фамилий в списке комитета. Если в результате в его
составе окажутся одни и те же люди, то по смыслу для нас это один и тот же
вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний
из 20 элементов по 5.
Иначе будут обстоять дела, если каждый член комитета изначально отвечает за
определенное направление работы. Тогда при одном и том же списочном составе
комитета, внутри него возможно 5! вариантов перестановок
, которые имеют значение. Количество
разных (и по составу, и по сфере ответственности) вариантов определяется в
этом случае числом размещений
из 20 элементов по 5.
Задачи для самопроверки
1. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5,
6, если цифры могут повторяться?
Т.к. число четное на третьем месте может стоять 0, 2, 4, 6, т.е. четыре цифры. На втором месте может стоять любая из семи цифр. На первом месте может стоять любая из семи цифр кроме нуля, т.е. 6 возможностей. Результат =4*7*6=168.
2. Сколько существует пятизначных чисел, которые одинаково читаются слева
направо и справа налево?
На первом месте может стоять любая цифра кроме 0, т.е. 9 возможностей. На втором месте может стоять любая цифра, т.е. 10 возможностей. На третьем месте тоже может стоять любая цифра из, т.е. 10 возможностей. Четвертая и пятая цифры определены заранее, они совпадают с первой и второй, следовательно, число таких чисел 9*10*10=900.
3. В классе десять предметов и пять уроков в день. Сколькими способами можно
составить расписание на один день?
4. Сколькими способами можно выбрать 4 делегата на конференцию, если в группе
20 человек?
n = C 20 4 = (20!)/(4!*(20-4)!)=(16!*17*18*19*20)/((1*2*3*4)*(16!))=(17*18*19*20)/(1*2*3*4)=4845.
5. Сколькими способами можно разложить восемь различных писем по восьми
различным конвертам, если в каждый конверт кладется только одно письмо?
В первый конверт можно положить 1 из восьми писем, во второй одно из семи оставшихся, в третий одно из шесть т.д. n = 8! = 1*2*3*4*5*6*7*8 = 40320.
6. Из трех математиков и десяти экономистов надо составить комиссию,
состоящую из двух математиков и шести экономистов. Сколькими способами это
можно сделать?
Ключевые понятия
Для расчета возможных комбинаций из 6 цифр необходимо учесть следующие ключевые понятия:
- Возможные комбинации: в данном контексте это все различные варианты, которые можно получить из 6 цифр.
- Расчеты: процесс определения количества возможных комбинаций путем математических операций.
- Из: указывает на исходный набор цифр, из которых формируются комбинации.
- Сколько: используется для задания вопроса о количестве возможных комбинаций.
- Цифры: числа от 0 до 9, используемые для составления комбинаций.
- 6: указывает на количество цифр, которые необходимо использовать при формировании комбинаций.
Формула для подсчета количества комбинаций
Для того чтобы посчитать количество комбинаций в 6-значном пароле из цифр, мы можем использовать формулу комбинаторики.
В данном случае у нас есть 10 возможных цифр, которые можно использовать. Таким образом, каждая цифра может принимать 10 возможных значений.
Поскольку пароль состоит из 6 цифр, то общее количество комбинаций можно посчитать, умножив количество возможных значений каждой цифры на саму себя 6 раз.
То есть, общее количество комбинаций в 6-значном пароле из цифр равно 10 * 10 * 10 * 10 * 10 * 10, или 10^6.
Итак, общее количество комбинаций в 6-значном пароле из цифр составляет 1 миллион.
| Цифра | Количество возможных значений |
|---|---|
| 1 | 10 |
| 2 | 10 |
| 3 | 10 |
| 4 | 10 |
| 5 | 10 |
| 6 | 10 |
Популярные методы взлома паролей
| Метод | Описание |
|---|---|
| Словарная атака | Взломщик использует специальные программы, которые перебирают слова из словарей, чтобы найти совпадение с паролем. Этот метод основывается на том факте, что многие люди используют слабые пароли на основе известных или распространенных слов. |
| Атака перебором | Этот метод основывается на простой итерации через все возможные комбинации символов и проверке каждой комбинации на соответствие паролю. Он особенно эффективен, когда пароль состоит только из цифр. |
| Фишинг | Фишинг — это метод, при котором злоумышленник создает поддельный веб-сайт или отправляет маскирующее письмо, в котором просит пользователей ввести свои учетные данные. Если пользователь проведет фишинговую атаку и введет свой пароль на поддельном сайте, злоумышленнику будет известен пароль. |
| Брутфорс | Брутфорс — это метод, при котором злоумышленник пробует все возможные комбинации символов для взлома пароля. Этот метод очень медленный и трудоемкий, но может быть эффективным, особенно если пароль несложный и короткий. |
| Социальная инженерия | Этот метод основывается на манипулировании людьми, чтобы они раскрыли свои учетные данные. Злоумышленник может использовать различные тактики, такие как представление в виде представителя службы поддержки или кража личности, чтобы убедить человека раскрыть свой пароль. |
Всегда важно использовать надежные пароли и следить за их безопасность. Введение двухфакторной аутентификации и регулярная смена паролей может помочь защитить вашу информацию
Важность создания уникальных паролей из комбинаций цифр
Цифровые пароли являются неотъемлемой частью нашего повседневного существования в мире онлайн-сервисов. От социальных сетей до интернет-банкинга, от электронной почты до онлайн-магазинов — все это требует пароля для доступа к аккаунту. Именно поэтому создание надежных, уникальных паролей является необходимостью.
Уникальные пароли, состоящие из комбинаций цифр, обладают несколькими преимуществами. Во-первых, они сложнее поддаются взлому и угадыванию, так как комбинации цифр являются более многообразными, чем простые слова или фразы. Во-вторых, они могут быть легко запомнены, если использовать особые ассоциации для каждой цифры.
Создание уникальных паролей можно осуществлять на основе изначальных комбинаций цифр, которые могут быть найдены в номерах телефонов. Например, можно использовать последовательность из 6 цифр номера телефона, чтобы создать уникальный пароль
При этом важно обеспечить сложность пароля путем добавления разных символов и использования регистра букв
К сожалению, множество пользователей всё еще предпочитает использовать простые пароли, такие как «123456» или «qwerty». Такие пароли являются наиболее уязвимыми и становятся простой мишенью для злоумышленников. Именно поэтому создание уникальных паролей из комбинаций цифр становится неотъемлемым аспектом обеспечения безопасности в нашем цифровом мире.
- Используйте минимум 8 символов в пароле.
- Используйте комбинацию цифр, букв разного регистра и специальных символов.
- Избегайте использования словарных слов и высокопопулярных фраз.
- Не используйте персональные данные, такие как даты рождения или имена семьи.
В целом, создание уникальных паролей из комбинаций цифр является важным шагом в обеспечении безопасности нашей цифровой жизни. Надежные пароли помогут предотвратить несанкционированный доступ к нашей личной и финансовой информации, защитить нас от киберпреступников и обеспечить надежность наших онлайн-аккаунтов.




























